题目内容
若x∈(e-1,1),a=lnx,b=2lnx,c=ln3x,则 ( )
| A.b<a<c | B.c<a<b | C.a<b<c | D.b<c<a |
A
根据函数的单调性,求a的范围,用比较法,比较a、b和a、c的大小.
解:因为a=lnx在(0,+∞)上单调递增,
故当x∈(e-1,1)时,a∈(-1,0),
于是b-a=2lnx-lnx=lnx<0,从而b<a.
又a-c=lnx-ln3x=a(1+a)(1-a)<0,从而a<c.
综上所述,b<a<c.
故选A
解:因为a=lnx在(0,+∞)上单调递增,
故当x∈(e-1,1)时,a∈(-1,0),
于是b-a=2lnx-lnx=lnx<0,从而b<a.
又a-c=lnx-ln3x=a(1+a)(1-a)<0,从而a<c.
综上所述,b<a<c.
故选A

练习册系列答案
相关题目
 的图象过点(0,
的图象过点(0, ),且
),且 的解集为(1,3)。
的解集为(1,3)。 的解析式;
的解析式; ,
, 的最值。
的最值。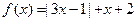 ,
,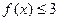 ;
;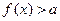 的解集为R,求
的解集为R,求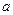 的取值范围。
的取值范围。 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值 万元与技术改造投入
万元与技术改造投入 万元之间满足:①
万元之间满足:① 成正比;②当
成正比;②当 时,
时, ,并且技术改造投入满足
,并且技术改造投入满足 ,其中
,其中 为常数且
为常数且 .
. 表达式及定义域;
表达式及定义域; 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则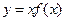 是
是 :
: ,若
,若  +
+
 ,
, 在
在 上有两个零点,则实数
上有两个零点,则实数 的取值范围是 ( )
的取值范围是 ( )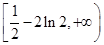



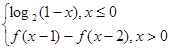 ,则f(2012)的值为( )
,则f(2012)的值为( )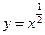 ,②
,②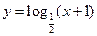 ,③
,③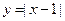 , ④
, ④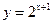 ,期中在区间(0,1)上单调递减的函数序号是( )
,期中在区间(0,1)上单调递减的函数序号是( ) 的图像大致为( ).
的图像大致为( ).