题目内容
如图,已知圆 ,经过椭圆
,经过椭圆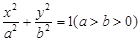 的右焦点F及上顶点B,过圆外一点
的右焦点F及上顶点B,过圆外一点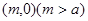 倾斜角为
倾斜角为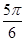 的直线
的直线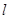 交椭圆于C,D两点,
交椭圆于C,D两点,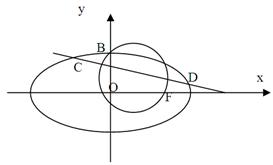
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
(1) ;(2)
;(2)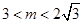
解析试题分析:(1)因为右焦点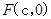 和上顶点
和上顶点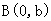 在圆
在圆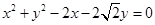 上,代入圆的方程,得
上,代入圆的方程,得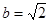 ,
, ,进而求得
,进而求得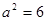 ,从而确定椭圆的方程;(1)涉及直线和圆锥曲线的位置关系问题,往往会用到结合根与系数的关系,利用“设而不求”的技巧,确定参数的值或范围.该题中,设直线
,从而确定椭圆的方程;(1)涉及直线和圆锥曲线的位置关系问题,往往会用到结合根与系数的关系,利用“设而不求”的技巧,确定参数的值或范围.该题中,设直线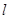 的方程
的方程 ,并和椭圆方程联立,得关于
,并和椭圆方程联立,得关于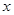 的一元二次方程,并注意隐函条件
的一元二次方程,并注意隐函条件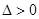 ,设交点
,设交点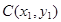 ,
,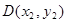 ,构造向量
,构造向量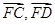 ,由题意得,
,由题意得,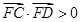 ,得关于
,得关于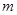 的不等式,解不等式即得参数
的不等式,解不等式即得参数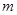 的取值范围.
的取值范围.
试题解析:(1)∵圆G: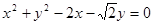 经过点F、B.∴F(2,0),B(0,
经过点F、B.∴F(2,0),B(0,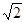 ),∴
),∴ ,
,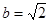 .∴
.∴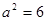 .故椭圆的方程为
.故椭圆的方程为 .
.
(2)设直线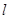 的方程为
的方程为 .
.
由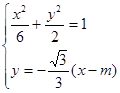 消去
消去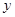 得
得 .
.
设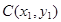 ,
,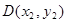 ,则
,则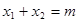 ,
,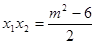 , 7分
, 7分
∴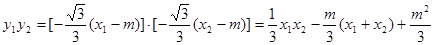 .
.
∵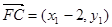 ,
, ,
,
∴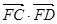 =
=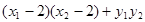
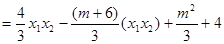 =
= .
.
∵点F在圆G的外部,∴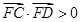 ,
,
即 ,解得
,解得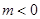 或
或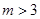 .由△=
.由△= ,解得
,解得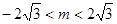 .又
.又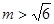 ,
, ,∴
,∴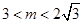 .
.
考点:1、椭圆的标准方程;2、直线和椭圆的位置关系;3、点和圆的位置关系.

练习册系列答案
相关题目
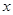 轴上的椭圆
轴上的椭圆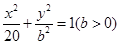 经过点
经过点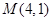 ,直线
,直线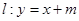
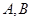 不同的两点.
不同的两点.
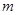 的取值范围;
的取值范围;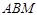 是以
是以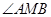 为直角的直角三角形,若存在,求出
为直角的直角三角形,若存在,求出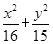 =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合.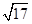 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.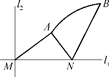
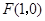 ,直线
,直线 ,
, 为平面上的动点,过点
为平面上的动点,过点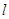 的垂线,垂足为点
的垂线,垂足为点 ,且
,且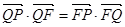 .
.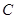 的方程;
的方程;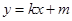 与曲线
与曲线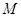 ,且与直线
,且与直线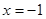 相交于点
相交于点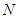 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点 ,使得以
,使得以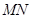 为直径的圆恒过此定点
为直径的圆恒过此定点 =1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.
=1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线. ,连结椭圆的四个顶点得到的菱形的面积为4.
,连结椭圆的四个顶点得到的菱形的面积为4. ,求直线l的倾斜角.
,求直线l的倾斜角. +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2: ,
, ),Q(
),Q(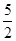 ,1),求椭圆C1的方程;
,1),求椭圆C1的方程; =1(a>0,b>0)的两条渐近线方程为y=±
=1(a>0,b>0)的两条渐近线方程为y=±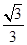 x,若顶点到渐近线的距离为1,求双曲线方程.
x,若顶点到渐近线的距离为1,求双曲线方程.