题目内容
(2012•泰安一模)为了增强学生的环境意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理,制成下表:
| 成绩 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100) |
| 频数 |
2 |
3 |
14 |
15 |
12 |
4 |
(I)作出被抽查学生成绩的频率分布直方图;
(II)若从成绩在[40,50)中选一名学生,从成绩在[90,100)中选出2名学生,共3名学生召开座谈会,求[40,50)组中学生A
1和[90,100)组中学生B
1同时被选中的概率?
分析:(I)由表格求出竞赛成绩落在各个区间内的频率,进而得到频率分布直方图中各组的纵坐标,从而画出频率分布直方图.
(II)所有的选法共有
•=12种,其中[40,50)组中学生A
1和[90,100)组中学生B
1同时被选中的选法有
••=3种,由此求得所求事件的概率.
解答:解:(I)由表格可知,竞赛成绩落在各个区间内的频率分别为
、
、
、
、
、
.
故频率分布直方图中各组的纵坐标分别为0.004、0.006、0.028、0.030、0.024、0.008,
被抽查学生成绩的频率分布直方图如图所示:

(II)所有的选法共有
•=12种,其中[40,50)组中学生A
1和[90,100)组中学生B
1同时被选中的选法有
••=3种,
故[40,50)组中学生A
1和[90,100)组中学生B
1同时被选中的概率为
=
.
点评:本题主要考查等可能事件的概率,频率分步直方图的画法,属于中档题.
练习册系列答案
相关题目



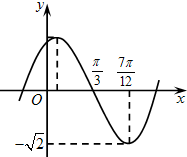 (2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则
(2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则