题目内容
某高级中学共有学生2000名,各年级男、女生人数如下表:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知y≥245,z≥245,求高三年级中女生不比男生多的概率.
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知y≥245,z≥245,求高三年级中女生不比男生多的概率.
分析:(1)先根据抽到高二年级女生的概率是0.19,求出高二女生的人数,可求出x值,
(2)再用全校的人数减去高一和高二的人数,得到高三的人数,全校要抽取48人,做出每个个体被抽到的概率,做出高三被抽到的人数.
(3)设出高三年级女生比男生多的事件为A,高三年级女生,男生数记为(y,z),因为y+z=500,且y,z∈N,列举出基本事件空间包含的基本事件有共11个,事件A包含的基本事件数,得到结果.
(2)再用全校的人数减去高一和高二的人数,得到高三的人数,全校要抽取48人,做出每个个体被抽到的概率,做出高三被抽到的人数.
(3)设出高三年级女生比男生多的事件为A,高三年级女生,男生数记为(y,z),因为y+z=500,且y,z∈N,列举出基本事件空间包含的基本事件有共11个,事件A包含的基本事件数,得到结果.
解答:解:(1)∵
=0.19,∴x=380
(2)高三年级人数为y+z=2000-(373+377+380+370)=500
现用分层抽样的方法在全校抽取48名学生,
应在高三年级抽取的人数为
×50=12(名).
(2)设高三年级女生不比男生多的事件为A,高三年级女生,
男生数记为(y,z),由(2)知y+z=500,且y,z∈N,
基本事件空间包含的基本事件有
(245,255),(246,254),(247,253),(248,252),(249,251),(250,250),
(251,249),(252,258),(253,257),(254,256),(255,245),共11个.
事件A包含的基本事件有:
(250,250),(251,249),(252,258),(253,257),(254,256),(255,245),共6个.
∴P(A)=
| x |
| 2000 |
(2)高三年级人数为y+z=2000-(373+377+380+370)=500
现用分层抽样的方法在全校抽取48名学生,
应在高三年级抽取的人数为
| 48 |
| 2000 |
(2)设高三年级女生不比男生多的事件为A,高三年级女生,
男生数记为(y,z),由(2)知y+z=500,且y,z∈N,
基本事件空间包含的基本事件有
(245,255),(246,254),(247,253),(248,252),(249,251),(250,250),
(251,249),(252,258),(253,257),(254,256),(255,245),共11个.
事件A包含的基本事件有:
(250,250),(251,249),(252,258),(253,257),(254,256),(255,245),共6个.
∴P(A)=
| 6 |
| 11 |
点评:本题考查等可能事件的概率,考查分层抽样,是一个统计的综合题,题目运算量不大,也没有难理解的知识点,是一个基础题.

练习册系列答案
相关题目
(14分)某高级中学共有学生3000名,各年级男、女生人数如下表:
| 高一年级 | 高二年级 | 高三年级 |
女生 | 523 | x | y |
男生 | 487 | 490 | z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.17.
(1)问高二年级有多少名女生?
(2)现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少
名学生?(本小题满分12分)某高级中学共有学生2000名,各年级男、女生人数如下表:
|
|
高一年级 |
高二年级 |
高三年级 |
|
女生 |
373 |
|
|
|
男生 |
377 |
370 |
|
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求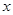 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高二年级抽取多少名?
(3)已知 ,
, ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.

