题目内容
求和：
= （
）.
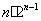
解析试题分析：设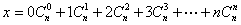
，
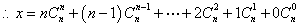，两式相加得，结合性质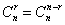
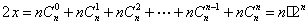
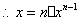
考点：数列求和
点评：本题结合组合数的性质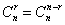采用倒序相加的方法求和，此方法一般适用于低n项与倒数第n项之和是同一个常数
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
励耘书业暑假衔接宁波出版社系列答案题目内容
求和：= （）.
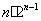
解析试题分析：设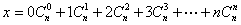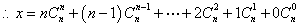，，两式相加得，结合性质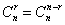
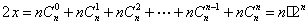
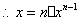
考点：数列求和
点评：本题结合组合数的性质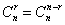采用倒序相加的方法求和，此方法一般适用于低n项与倒数第n项之和是同一个常数
励耘书业暑假衔接宁波出版社系列答案
轴上的整点），其运动规律为
或
。若该动点从原点出发，经过6步运动到（6,2）点，则有__________________种不同的运动轨迹。
的展开式中，x的系数是 。（用数字作答）
的展开式的各项系数之和为
，二项式系数之和为
，若
，则展开式中
的系数为___________
，则
的值为 ．
的展开式中常数项的值是 （数字作答）；
的最大自然数n= ．