题目内容
定义:若平面点集A中的任一个点(x0,y0),总存在正实数r,使得集合{(x,y)|
<r}⊆A,则称A为一个开集.给出下列集合:①(x,y)|x2+y2=1;②(x,y)|x+y+2≥0;③(x,y)|x+y<6;④{(x,y)|0<x2+(y-
)2<1}.其中是开集的是( )
| (x-x0)2+(y-y0)2 |
| 3 |
| A、①④ | B、②③ | C、②④ | D、③④ |
分析:根据开集的定义逐个验证选项,即可得到答案,:①:A={(x,y)|x2+y2=4}表示以原点为圆心,2为半径的圆,以圆上的点为圆心正实数r为半径的圆面不可能在该圆上,故不是开集,②在曲线x+y+2=0任意取点(x0,y0),以任意正实数r为半径的圆面,均不满足 {(x,y)|
<r}⊆A,故该集合不是开集;③点集A中的任一点(x0,y0),则该点到直线的距离为d,取r=d,满足条件,故是开集;④该平面点集A中的任一点(x0,y0),则该点到圆周上的点的最短距离为d,取r=d,则满足,{(x,y)|
<r}⊆A,故该集合是开集.从而得到答案.
| (x-x0)2+(y-y0)2 |
| (x-x0)2+(y-y0)2 |
解答:解:①:A={(x,y)|x2+y2=1}表示以原点为圆心,1为半径的圆,
则在该圆上任意取点(x0,y0),以任意正实数r为半径的圆面,均不满足 {(x,y)|
<r}⊆A
故①不是开集;
②A={(x,y)|x+y+2≥0},在曲线x+y+2=0任意取点(x0,y0),以任意正实数r为半径的圆面,均不满足 {(x,y)|
<r}⊆A,故该集合不是开集;
③A={(x,y)|x+y<6}平面点集A中的任一点(x0,y0),则该点到直线的距离为d,取r=d,则满足,{(x,y)|
<r}⊆A,故该集合是开集;
④A={(x,y)|0<x2+(y-
)2<1}表示以点(0,
)为圆心,1为半径除去圆心和圆周的圆面,在该平面点集A中的任一点(x0,y0),则该点到
圆周上的点的最短距离为d,取r=d,则满足,{(x,y)|
<r}⊆A,故该集合是开集.
故选D.
则在该圆上任意取点(x0,y0),以任意正实数r为半径的圆面,均不满足 {(x,y)|
| (x-x0)2+(y-y0)2 |
故①不是开集;
②A={(x,y)|x+y+2≥0},在曲线x+y+2=0任意取点(x0,y0),以任意正实数r为半径的圆面,均不满足 {(x,y)|
| (x-x0)2+(y-y0)2 |
③A={(x,y)|x+y<6}平面点集A中的任一点(x0,y0),则该点到直线的距离为d,取r=d,则满足,{(x,y)|
| (x-x0)2+(y-y0)2 |
④A={(x,y)|0<x2+(y-
| 3 |
| 3 |
圆周上的点的最短距离为d,取r=d,则满足,{(x,y)|
| (x-x0)2+(y-y0)2 |
故选D.
点评:此题是个中档题.本题属于集合的新定义型问题,考查学生即时掌握信息,解决问题的能力.正确理解好集的定义是解决本题的关键.

练习册系列答案
相关题目
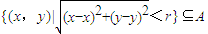 ,则称A为一个开集.给出下列集合:①(x,y)|x2+y2=4;②(x,y)|x+y-2>0;③(x,y)||x+y|≤2;④
,则称A为一个开集.给出下列集合:①(x,y)|x2+y2=4;②(x,y)|x+y-2>0;③(x,y)||x+y|≤2;④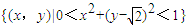 .其中是开集的是( )
.其中是开集的是( )