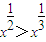题目内容
下列四个命题：
①任意x∈（0，+∞），使得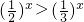
；
②存在x∈（0，1），使得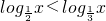
；
③任意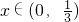
，使得
；
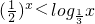④存在x∈（0，+∞），使得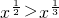
其中真命题的序号是________．
①③④
分析：①由幂函数的性质进行判断；②由对数函数的性质进行判断；③由指数函数和对数函数的性质进行判断；④举实例进行判断．
解答：①∵x∈（0，+∞），∴由幂函数的性质，得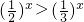，故①是真命题；
②∵x∈（0，1），∴由对数函数的性质，得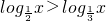
，故②是假命题；
③∵，∴（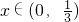
）x＜1，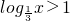
，
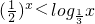∴，故③是真命题；
④∵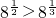
，
∴存在x∈（0，+∞），使得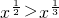，故④是真命题．
故答案为：①③④．
点评：本题考查命题的真假判断，是基础题．解题时要认真审题，仔细解答，注意幂函数、指数函数、对数函数的性质进行判断．
分析：①由幂函数的性质进行判断；②由对数函数的性质进行判断；③由指数函数和对数函数的性质进行判断；④举实例进行判断．
解答：①∵x∈（0，+∞），∴由幂函数的性质，得
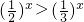，故①是真命题；②∵x∈（0，1），∴由对数函数的性质，得
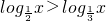，故②是假命题；③∵
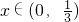，∴（）x＜1，，∴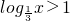
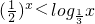，故③是真命题；④∵
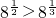，∴存在x∈（0，+∞），使得
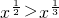，故④是真命题．故答案为：①③④．
点评：本题考查命题的真假判断，是基础题．解题时要认真审题，仔细解答，注意幂函数、指数函数、对数函数的性质进行判断．
练习册系列答案
相关题目
； 
；
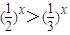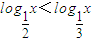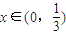，使得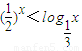
；