题目内容
在平面直角坐标系xOy中,过点A(-2,-1)椭圆C∶ =1(a>b>0)的左焦点为F,短轴端点为B1、B2,
=1(a>b>0)的左焦点为F,短轴端点为B1、B2,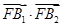 =2b2.
=2b2.
(1)求a、b的值;
(2)过点A的直线l与椭圆C的另一交点为Q,与y轴的交点为R.过原点O且平行于l的直线与椭圆的一个交点为P.若AQ·AR=3OP2,求直线l的方程.
 =1(a>b>0)的左焦点为F,短轴端点为B1、B2,
=1(a>b>0)的左焦点为F,短轴端点为B1、B2,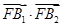 =2b2.
=2b2.(1)求a、b的值;
(2)过点A的直线l与椭圆C的另一交点为Q,与y轴的交点为R.过原点O且平行于l的直线与椭圆的一个交点为P.若AQ·AR=3OP2,求直线l的方程.
(1)a=2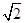 ,b=
,b=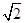 (2)当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0.
(2)当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0.
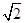 ,b=
,b=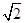 (2)当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0.
(2)当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0.(1)因为F(-c,0),B1(0,-b),B2(0,b),所以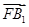 =(c,-b),
=(c,-b),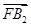 =(c,b).
=(c,b).
因为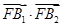 =2b2,
=2b2,
所以c2-b2=2b2.①
因为椭圆C过A(-2,-1),代入得,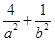 =1.②
=1.②
由①②解得a2=8,b2=2.
所以a=2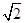 ,b=
,b=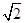 .
.
(2)由题意,设直线l的方程为y+1=k(x+2).
由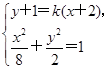 得(x+2)[(4k2+1)(x+2)-(8k+4)]=0.
得(x+2)[(4k2+1)(x+2)-(8k+4)]=0.
因为x+2≠0,所以x+2=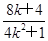 ,即xQ+2=
,即xQ+2=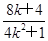 .
.
由题意,直线OP的方程为y=kx.
由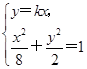 得(1+4k2)x2=8.则
得(1+4k2)x2=8.则 =
=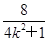 ,
,
因为AQ·AR=3OP2.所以|xQ-(-2)|×|0-(-2)|=3 .
.
即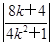 ×2=3×
×2=3×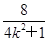 .
.
解得k=1,或k=-2.
当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0
 =(c,-b),
=(c,-b),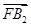 =(c,b).
=(c,b).因为
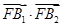 =2b2,
=2b2,所以c2-b2=2b2.①
因为椭圆C过A(-2,-1),代入得,
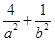 =1.②
=1.②由①②解得a2=8,b2=2.
所以a=2
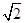 ,b=
,b=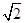 .
.(2)由题意,设直线l的方程为y+1=k(x+2).
由
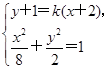 得(x+2)[(4k2+1)(x+2)-(8k+4)]=0.
得(x+2)[(4k2+1)(x+2)-(8k+4)]=0.因为x+2≠0,所以x+2=
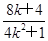 ,即xQ+2=
,即xQ+2=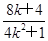 .
.由题意,直线OP的方程为y=kx.
由
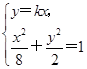 得(1+4k2)x2=8.则
得(1+4k2)x2=8.则 =
=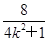 ,
,因为AQ·AR=3OP2.所以|xQ-(-2)|×|0-(-2)|=3
 .
.即
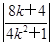 ×2=3×
×2=3×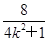 .
.解得k=1,或k=-2.
当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0

练习册系列答案
相关题目
 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,
=1(a>b>0)的左、右焦点分别为F1,F2,点A在椭圆C上,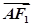 ·
· =0,3|
=0,3| |·|
|·| |=-5
|=-5 ·
· =
= ·
· ?若存在,求出实数m的取值范围;若不存在,说明理由.
?若存在,求出实数m的取值范围;若不存在,说明理由. 的离心率是
的离心率是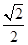 ,
, 分别是椭圆
分别是椭圆 的左、右两个顶点,点
的左、右两个顶点,点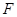 是椭圆
是椭圆 是
是 轴上位于
轴上位于 右侧的一点,且满足
右侧的一点,且满足 .
.
 ,再作直线
,再作直线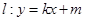 与椭圆
与椭圆 ,直线
,直线 交直线
交直线 .求证:以线段
.求证:以线段 为直径的圆恒过定点,并求出定点的坐标.
为直径的圆恒过定点,并求出定点的坐标. ,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知
,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知 =λ
=λ ,
, =λ
=λ ,其中0<λ<1.
,其中0<λ<1.
 +y2=1上;
+y2=1上;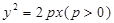 ,其准线方程为
,其准线方程为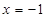 ,过准线与
,过准线与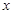 轴的交点
轴的交点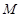 做直线
做直线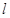 交抛物线于
交抛物线于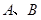 两点.
两点.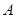 为
为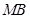 中点,求直线
中点,求直线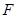 ,当
,当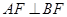 时,求
时,求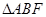 的面积.
的面积. (a为长半轴,c为半焦距)上.
(a为长半轴,c为半焦距)上. .
. 轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且
轴上,焦距为2,直线n:x-y-1=0与椭圆C交于A、B两点,F1是左焦点,且 ,则椭圆C的标准方程是
,则椭圆C的标准方程是  =1(a>b>0)上两点,已知m=
=1(a>b>0)上两点,已知m= ,n=
,n= ,若m·n=0且椭圆的离心率e=
,若m·n=0且椭圆的离心率e= ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.