题目内容
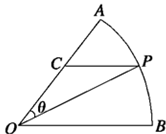
如图所示,扇形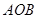 ,圆心角
,圆心角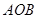 的大小等于
的大小等于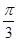 ,半径为
,半径为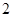 ,在半径
,在半径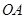 上有一动点
上有一动点 ,过点
,过点 作平行于
作平行于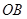 的直线交弧
的直线交弧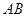 于点
于点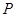 .
.
(1)若 是半径
是半径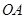 的中点,求线段
的中点,求线段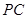 的大小;
的大小;
(2)设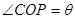 ,求△
,求△ 面积的最大值及此时
面积的最大值及此时 的值.
的值.
(1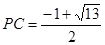 )(2)
)(2) 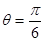 时,
时,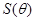 取 得最大值为
取 得最大值为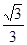 .
.
解析试题分析:解:(1)在△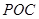 中,
中, ,
,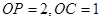
由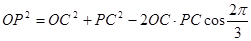
得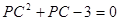 ,解得
,解得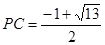 .
.
(2)∵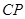 ∥
∥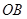 ,∴
,∴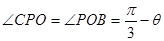 ,
,
在△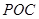 中,由正弦定理得
中,由正弦定理得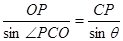 ,即
,即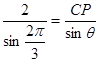
∴ ,又
,又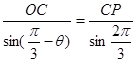
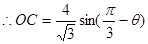 .
.
解法一:记△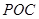 的面积为
的面积为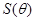 ,则
,则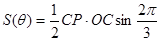 ,
, 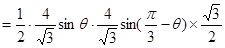
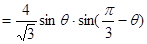
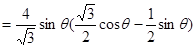
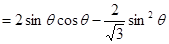
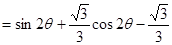
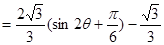
∴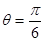 时,
时,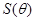 取得最大值为
取得最大值为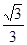 .
.
解法二: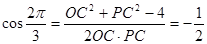
即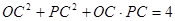 ,又
,又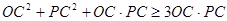 即
即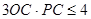
当且仅当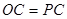 时等号成立,
时等号成立,
所以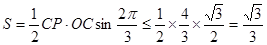
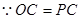 ∴
∴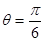 时,
时,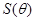 取 得最大值为
取 得最大值为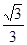 .
.
考点:余弦定理和三角形面积
点评:主要是考查了解三角形边角的转换,以及三角形面积公式的求解的综合运用,属于基础题。

练习册系列答案
相关题目
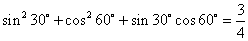 ;
;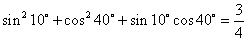 ;
;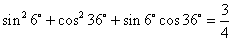 .
. .
.  的值.
的值.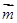 =(
=( sin
sin ,1),
,1),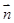 =(cos
=(cos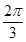 -x)的值;
-x)的值;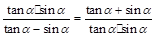 .
.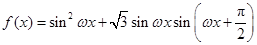 (
(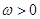 )的最小正周期为
)的最小正周期为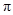 .
.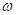 的值;
的值; 在区间
在区间 上的取值范围.
上的取值范围. 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为 ,
, ,
,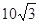 .
.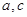 的值;(6分)
的值;(6分)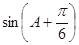 .(4分)
.(4分)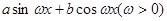 的周期为
的周期为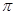 ,且对一切x
,且对一切x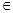 R,都有f(x)
R,都有f(x)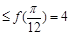 ;
; 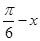 ),求函数g(x)的单调增区间;
),求函数g(x)的单调增区间;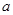 ,使得函数
,使得函数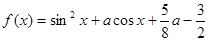 在闭区间
在闭区间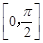 上的最大值为1?若存在,求出对应的
上的最大值为1?若存在,求出对应的