题目内容
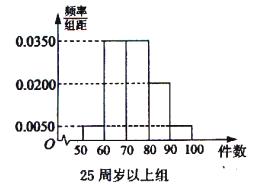
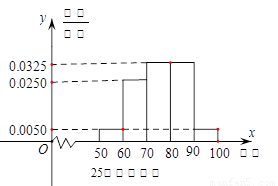
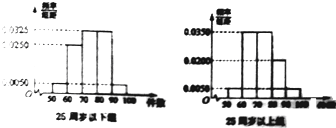 某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数:
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”.此工厂有一个优良传统,要求1名“菜鸟”必须找一位“生产能手”组成“师徒组”.从样本中的“生产能手”和“菜鸟”中任意抽取2人,求2人恰好能组成“师徒组”的概率.
分析:(1)根据工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名,可得样本中有25周岁以上组工人100×
人,累加频率分布直方图中各组组中及频率,可估算出“25周岁以上(含25周岁)组”的日生产量平均数.
(2)列举出所有从“生产能手”和“菜鸟”中随机抽取2名工人的基本事件个数,及2人恰好能组成师徒的可能结果,代入古典概型概论公式,可得答案.
| 300 |
| 300+200 |
(2)列举出所有从“生产能手”和“菜鸟”中随机抽取2名工人的基本事件个数,及2人恰好能组成师徒的可能结果,代入古典概型概论公式,可得答案.
解答:解:(1)由已知得,样本中有25周岁以上组工人100×
=60名
样本中“25周岁以上(含25周岁)组”的日生产量平均数为
55×0.05+65×0.35+75×0.35+85×0.20+95×0.05=73.5
(2)“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”的工人有6×0.05=3人,
分别记为A,B,C;
“25周岁以下组”中日平均生产不足60件的称为“菜鸟”的工人有4×0.05=2人,
分别记为D,E;
从中随机抽取2名工人,所有的可能的结果共有10种,分别为:
(A,B),(A,C),(A,D),(A,E),(B,C),
(B,D),(B,E),(C,D),(C,E),(D,E)
其中2人恰好能组成师徒的可能结果共有6中,分别为:
(A,D),(A,E),(B,D),(B,E),(C,D),(C,E),
故2人恰好能组成“师徒组”的概率P=
=
| 300 |
| 300+200 |
样本中“25周岁以上(含25周岁)组”的日生产量平均数为
55×0.05+65×0.35+75×0.35+85×0.20+95×0.05=73.5
(2)“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”的工人有6×0.05=3人,
分别记为A,B,C;
“25周岁以下组”中日平均生产不足60件的称为“菜鸟”的工人有4×0.05=2人,
分别记为D,E;
从中随机抽取2名工人,所有的可能的结果共有10种,分别为:
(A,B),(A,C),(A,D),(A,E),(B,C),
(B,D),(B,E),(C,D),(C,E),(D,E)
其中2人恰好能组成师徒的可能结果共有6中,分别为:
(A,D),(A,E),(B,D),(B,E),(C,D),(C,E),
故2人恰好能组成“师徒组”的概率P=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题考查列举法求事件发生的概率,分层抽样,利用频率分布直方图估计平均数,是统计和概率的综合应用,难度不大,属于基础题.

练习册系列答案
相关题目




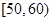 ,
, ,
, ,
, ,
,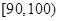 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图. 的列联表,并判断是否有
的列联表,并判断是否有 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?