题目内容
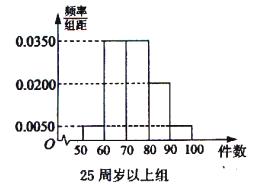
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60), [60,70), [70,80), [80,90), [90,100), 分别加以统计,得到如图所示的频率分布直方图。
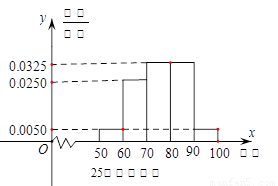

(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
(Ⅰ)样本中有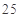 周岁以上组工人
周岁以上组工人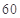 名,平均数为73.5;(2)
名,平均数为73.5;(2)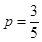 .
.
【解析】
试题分析:(Ⅰ)分层抽样实质上就是按比例抽样,根据比例即可求得样本中有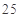 周岁以上组工人的人数;
周岁以上组工人的人数;
根据频率分布直方图求平均数的公式为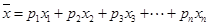 ,其中
,其中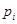 为第
为第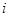 组数据的频率,
组数据的频率,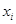 是第
是第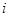 组数据的中间值.由此公式可得样本中“25周岁以上(含25周岁)组”的日生产量平均数.
组数据的中间值.由此公式可得样本中“25周岁以上(含25周岁)组”的日生产量平均数.
(2)首先根据频率求出样本中“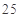 周岁以上组”中的 “生产能手”的人数和 “25周岁以下组”中的“菜鸟”工人的人数,用字母表示这些工人,然后一一列出所有可能结果,再数出改好能组成师徒组的可能结果,由古典概型概率公式求得所求概率.
周岁以上组”中的 “生产能手”的人数和 “25周岁以下组”中的“菜鸟”工人的人数,用字母表示这些工人,然后一一列出所有可能结果,再数出改好能组成师徒组的可能结果,由古典概型概率公式求得所求概率.
试题解析:(Ⅰ)由已知得,样本中有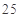 周岁以上组工人
周岁以上组工人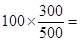
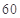 名 4分
名 4分
样本中“25周岁以上(含25周岁)组”的日生产量平均数为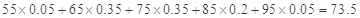 5分
5分
(2)由样本中“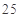 周岁以上组”中日平均生产90件及90件以上的 “生产能手”工人有
周岁以上组”中日平均生产90件及90件以上的 “生产能手”工人有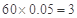 (人), 记为
(人), 记为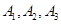 .“25周岁以下组”中日平均生产不足60件的称为“菜鸟”工人有
.“25周岁以下组”中日平均生产不足60件的称为“菜鸟”工人有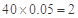 (人),记为
(人),记为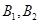 .
8分
.
8分
从中随机地抽取两人,所有可能的结果共有以下10种:
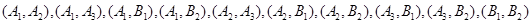 10分
10分
其中,2人恰好能组成师徒组的可能结果共有以下6种:
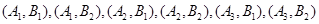 .
.
由古典概型的概率公式得所求概率为: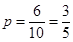 12分
12分
考点:1、频率分布直方图;2、古典概型.

 名校课堂系列答案
名校课堂系列答案
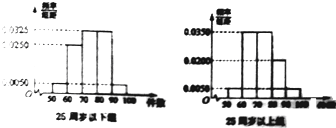 某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图.

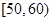 ,
, ,
, ,
, ,
,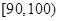 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图. 的列联表,并判断是否有
的列联表,并判断是否有 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?