题目内容
“1<a<2”是“对任意的正数x,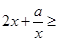 2”的
2”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:当1<a<2,由基本不等式得:对任意的正数x, ,所以
,所以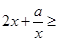 2。若
2。若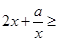 2,则
2,则 。所以“1<a<2”是“对任意的正数x,
。所以“1<a<2”是“对任意的正数x,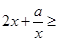 2”的充分不必要条件。
2”的充分不必要条件。
考点:基本不等式;充分、必要、充要条件的判断。
点评:熟练灵活应用基本不等式是做本题的前提条件。属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“a和b都不是偶数”的否定形式是 ( )
| A.a和b至少有一个是偶数 | B.a和b至多有一个是偶数 |
| C.a是偶数,b不是偶数 | D.a和b都是偶数 |
设平面 与平面
与平面 相交于直线
相交于直线 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若 ,则“
,则“ ”是“
”是“ ”的( )条件( )
”的( )条件( )
| A.充分而不必要 | B.必要而不充分 | C.充要 | D.既不充分也不必要 |
命题“ ”的否定是( )
”的否定是( )
A. | B. |
C. | D. |
命题“ ,
, ”的否定是( )
”的否定是( )
A. , , | B. , , |
C. , , | D. , , |
下列各命题中正确的命题是
①“若 都是奇数,则
都是奇数,则 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若 不是偶数,则
不是偶数,则 都不是奇数”;
都不是奇数”;
② 命题 “ ”的否定是“
”的否定是“ ” ;
” ;
③ “函数 的最小正周期为
的最小正周期为 ” 是“
” 是“ ”的必要不充分条件;
”的必要不充分条件;
④“平面向量 与
与 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ” .
” .
| A.②③ | B.①②③ | C.①②④ | D.③④ |
下列有关命题的说法中,正确的是 ( )
A.命题 的否命题为 的否命题为 。 。 |
B. 的充分不必要条件 。 的充分不必要条件 。 |
C.命题 。 。 |
D.命题 的逆命题为真命题。 的逆命题为真命题。 |
 是定义在
是定义在 上的函数,
上的函数, 则“
则“ 均为偶函数”是“
均为偶函数”是“ 为偶函数”的( )
为偶函数”的( )
| A.充要条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |