题目内容
已知抛物线C1:y=x2,椭圆C2:x2+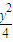 =1.
=1.(1)设l1,l2是C1的任意两条互相垂直的切线,并设l1∩l2=M,证明:点M的纵坐标为定值;
(2)在C1上是否存在点P,使得C1在点P处切线与C2相交于两点A、B,且AB的中垂线恰为C1的切线?若存在,求出点P的坐标;若不存在,说明理由.
【答案】分析:(1)求导,设切点分别为(x1,x12),(x2,x22),求出直线l1,l2的方程,根据l1⊥l2可得结果;
(2)设P(x,x2),写出C1在点P处切线方程,联立它与椭圆的方程,消去y,得到关于x一元二次方程,△>0,利用韦达定理和(1)的结论即可求出点P的坐标.
解答:解:(1)y′=2x,
设切点分别为(x1,x12),(x2,x22)
则l1方程为y-x12=2x1(x-x1)
即y=2x1x-x12 ①
l2方程为y=2x2x-x22 ②
由l1⊥l2得2x12x2=-1
即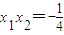
所以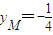 ,
,
即点M的纵坐标为定值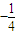 .
.
(2)设P(x,x2),
则C1在点P处切线方程为:y=2xx-x2
代入C2方程4x2+y2-4=0
得4x2+(2xx-x2)-4=0
即(4+4x2)x2-4x3x+x4-4=0
设A(x3,y3),B(x4,y4)
则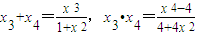
△=16x6-16(1+x2)(x4-4)=16(4+4x2-x4)>0 ③
由(1)知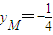
从而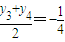 ,
,
即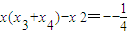
进而得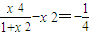
解得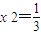 ,且满足③
,且满足③
所以这样点P存在,其坐标为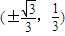 .
.
点评:此题是个难题.本题考查了椭圆与抛物线的标准方程、直线与圆锥曲线的位置关系,以及利用导数研究抛物线的切线方程,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,
(2)设P(x,x2),写出C1在点P处切线方程,联立它与椭圆的方程,消去y,得到关于x一元二次方程,△>0,利用韦达定理和(1)的结论即可求出点P的坐标.
解答:解:(1)y′=2x,
设切点分别为(x1,x12),(x2,x22)
则l1方程为y-x12=2x1(x-x1)
即y=2x1x-x12 ①
l2方程为y=2x2x-x22 ②
由l1⊥l2得2x12x2=-1
即
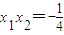
所以
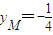 ,
,即点M的纵坐标为定值
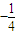 .
.(2)设P(x,x2),
则C1在点P处切线方程为:y=2xx-x2
代入C2方程4x2+y2-4=0
得4x2+(2xx-x2)-4=0
即(4+4x2)x2-4x3x+x4-4=0
设A(x3,y3),B(x4,y4)
则
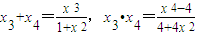
△=16x6-16(1+x2)(x4-4)=16(4+4x2-x4)>0 ③
由(1)知
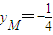
从而
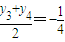 ,
,即
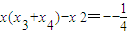
进而得
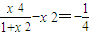
解得
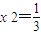 ,且满足③
,且满足③所以这样点P存在,其坐标为
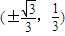 .
.点评:此题是个难题.本题考查了椭圆与抛物线的标准方程、直线与圆锥曲线的位置关系,以及利用导数研究抛物线的切线方程,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,

练习册系列答案
相关题目
已知抛物线C1:y=2x2与抛物线C2关于直线y=-x对称,则C2的准线方程为( )
A、x=
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|