题目内容

20．在等差数列{an}中，若a1+a2+…+a15=x，an-14+an-13+…+an=y，求Sn．

分析 利用等差数列的性质，结合等差数列的前n项和公式，即可求Sn．

解答 解：∵等差数列{an}中，a1+a2+…+a15=x，an-14+an-13+…+an=y，
∴15（a1+an）=x+y，
∴Sn=$\frac{n}{2}$（a1+an）=$\frac{n（x+y）}{30}$．

点评 本题考查等差数列的性质，等差数列的前n项和公式，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
10．若psinθ-qcosθ=$\sqrt{{p}^{2}+{q}^{2}}$（p，q为常数，且q≠0），求$\frac{pcosθ-2qsinθ}{3pcosθ-4qsinθ}$的值．
11．从装有十个红球和十个白球的罐子里任取2球，下列情况中互斥而不对立的两个事件是（　　）
A．至少有一个红球，至少有一个白球B．恰有一个红球，都是白球
C．至少有一个红球，都是白球D．至多有一个红球，都是红球
8．把一副扑克（除去大、小王）的52张随机均分给赵、钱、孙、李四家，A=赵家得到6张草花，B=孙家得到3张草花．
（1）计算P（B|A）；
（2）计算P（AB）．
15．若f（x）=（m-1）x2+2mx+3是偶函数，则f（x）的最大值是3．
5．已知△ABC的三个内角A，B，C的对边分别为a，b，c，cosC=$\frac{sinC+2sinB}{2sinA}$，求∠A的大小．
12．已知函数f（x）=$\frac{1}{2}$x2-2x+a2lnx，x∈（$\frac{a}{3}$，a）（a＞0）．
（1）当a=2时，求点P（1，f（1））处的切线方程；
（2）若函数y=f（x）在定义域上有最大值，求a的取值范围．
9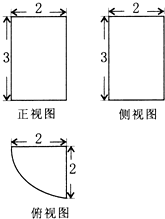．某空间几何体的三视图如图所示（其中俯视图的弧线为四分之一圆），则该几何体的表面积为（　　）
A．5π+4B．14π+4C．5π+12D．14π+12
10．已知椭圆C$：\;\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F1，F2，若等边△F1F2P的一个顶点P在椭圆C上，则椭圆C的离心率为$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网