题目内容
(09年临沂一模理)(12分)
如图,在直棱柱ABC-A1B1C1中,AC=BC=![]() AA1,∠ACB=90º,G为BB1的中点。
AA1,∠ACB=90º,G为BB1的中点。
(1)求证:平面A1CG⊥平面A1GC1;
(2)求平面ABC与平面A1GC所成锐二面角的平面角的余弦值。

解析:(I)证明:在直棱柱ABC-A1B1C1中,有A1C1⊥CC1。
∵ ∠ACB=90º,∴A1C1⊥C1B1,即A1C1⊥平面C1CBB1,
∵CG![]() 平面C1CBB1,∴A1C1⊥CG。┉┉┉┉┉┉┉┉2分
平面C1CBB1,∴A1C1⊥CG。┉┉┉┉┉┉┉┉2分
在矩形C1CBB1中,CC1=BB1=2BC,G为BB1的中点,
CG=![]() BC,C1G=
BC,C1G=![]() BC,CC1=2BC
BC,CC1=2BC
∴∠CGC1=90,即CG⊥C1G┉┉┉┉┉┉┉┉4分
而A1C1∩C1G=C1,
∴CG⊥平面A1GC1。
∴平面A1CG⊥平面A1GC1。┉┉┉┉┉┉┉┉6分
(II)由于CC1平面ABC,
∠ACB=90º,建立如图所示的空间坐标系,设AC=BC=CC1=a,则A(a,0,0),B(0,a,0)
A1(a,0,2a),G(0,a,a).
∴![]() =(a,0,2a),
=(a,0,2a),![]() =(0,a,a). ┉┉┉┉┉┉┉┉8分
=(0,a,a). ┉┉┉┉┉┉┉┉8分
设平面A1CG的法向量n1=(x1,y1,z1),
由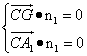 得
得
令z1=1,n1=(-2,-1,1). ┉┉┉┉┉┉┉┉9分
又平面ABC的法向量为n2=(0,0,1) ┉┉┉┉┉┉┉┉10分
设平面ABC与平面A1CG所成锐二面角的平面角为θ,
则 ┉┉┉┉┉┉┉┉11分
┉┉┉┉┉┉┉┉11分
即平面ABC与平面A1CG所成锐二面角的平面角的余弦值为![]() 。┉┉┉12分
。┉┉┉12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目