题目内容
某电视台举办的技能比赛节目中,每位参赛选手需参加两场比赛,两场比赛都胜出获得10万现金;若只胜一场,则奖励5万;两场都失利则无奖金.设甲选手每场比赛胜利的概率都为
且两场比赛之间相互独立,用ξ表示甲选手比赛结束后的奖金总额.
(I)求比赛结束后甲选手只胜一场的概率;
(Ⅱ)求ξ的分布列和数学期望.
| 1 | 2 |
(I)求比赛结束后甲选手只胜一场的概率;
(Ⅱ)求ξ的分布列和数学期望.
分析:(I)已知要求比赛结束后甲选手只胜一场的概率,即“甲胜第一场或第二场”,根据独立重复事件的概率公式,从而求出其概率;
(II)小组比赛中甲的得分为ξ可能值为0、5、10,分别求出其概率,再根据期望的公式进行求解.
(II)小组比赛中甲的得分为ξ可能值为0、5、10,分别求出其概率,再根据期望的公式进行求解.
解答:解:(I)设“比赛结束后甲选手只胜一场”为事件A,则P(A)=
×
×
=
;
(II)ξ的可能值为0,5,10.且P(ξ=0)=(
)2=
,P(ξ=5)=
,P(ξ=10)=(
)2=
,
ξ的分布列:
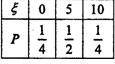
数学期望Eξ=0×
+5×
+10×
=5(万).
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(II)ξ的可能值为0,5,10.且P(ξ=0)=(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
ξ的分布列:

数学期望Eξ=0×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:此题主要考查离散随机变量的期望公式,这也是高考的热点问题,此题是一道基础题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
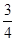 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是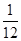 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是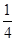 ,且三人答对这道题的概率互不影响.
,且三人答对这道题的概率互不影响.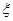 的分布列.
的分布列. 且两场比赛之间相互独立,用ξ表示甲选手比赛结束后的奖金总额.
且两场比赛之间相互独立,用ξ表示甲选手比赛结束后的奖金总额. ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是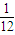 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 ,且三人答对这道题的概率互不影响.
,且三人答对这道题的概率互不影响.