题目内容
设命题甲:ax2+2ax+1>0的解集是实数集R;命题乙:0<a<1,则命题甲是命题乙成立的( )
| A、充分非必要条件 | B、必要非充分条件 | C、充要条件 | D、既非充分又非必要条件 |
分析:利用充分必要条件的判断方法判断两命题的推出关系,注意不等式恒成立问题的处理方法.
解答:解:ax2+2ax+1>0的解集是实数集R
①a=0,则1>0恒成立
②a≠0,则
,故0<a<1
由①②得0≤a<1.即命题甲?0≤a<1.因此甲推不出乙,而乙?甲,因此命题甲是命题乙成立的必要非充分条件.
故选B.
①a=0,则1>0恒成立
②a≠0,则
|
由①②得0≤a<1.即命题甲?0≤a<1.因此甲推不出乙,而乙?甲,因此命题甲是命题乙成立的必要非充分条件.
故选B.
点评:本题考查命题的充分必要性,考查不等式恒成立的等价关系.值域数形结合的思想和等价转化的思想的运用.

练习册系列答案
相关题目
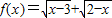 是函数.
是函数.