题目内容

给出下列命题：①若f（x）为增函数，则[f（x）]²也为增函数；②命题甲：ax²+2ax+1＞0的解集是R；命题乙：0＜a＜1，则命题甲是命题乙成立的充要条件；③设2^a=3，2^b=6，2^c=12，则a、b、c成等差数列．
其中正确命题的序号是

（注：把你认为正确命题的序号都填上）．

分析：通过举反例判断出①错，通过求出二次不等式恒成立的充要条件判断出②错，利用等差数列的定义判断出③对．

解答：解：对于①例如f（x）=x则[f（x）]²=x²，虽然f（x）是增函数但[f（x）]²不是增函数
对于②中的命题甲?a=0或

a＞0

△=4a2-4a＜0

?0≤a＜1故命题甲是命题乙成立的必要不充分条件
对于③∵（2^b）²=2^a•2^c，∴2b=a+c，∴a、b、c成等差数列
故③正确
故答案为：③

点评：本题考查等差数列的定义、二次不等式恒成立、举反例说明命题假是解决小题的重要方法．

练习册系列答案

大赢家考前巧复习系列答案

大中考系列答案

单元测评导评导测导考系列答案

单元测试卷湖南教育出版社系列答案

单元达标卷系列答案

单元过关目标检测卷系列答案

天舟文化单元练测卷系列答案

单元巧练章节复习手册系列答案

学习指导与评价系列答案

单元综合练习与检测AB卷系列答案

相关题目

给出下列命题：
①函数y=f（x-2）与函数y=f（2-x）的图象关于x=2对称；
②函数y=f（x）导函数为y=f′（x），若f′（x₀）=0，则f（x₀）必为函数y=f（x）的极值；
③函数y=sinx在一象限单调递增；
④y=tanx在其定义域内为单调增函数．
其中正确的命题序号为

给出下列命题：

(1)若＞0，则f(x)＞0；

(2)dx＝4；

(3)f(x)的原函数为F(x)，且F(x)是以T为周期的函数，则＝．

其中正确命题的个数为

1

2

3

0

(黄冈中学模拟)给出下列命题：

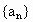A.若成等比数列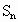，是前n项和，则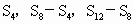成等比数列；

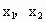B.已知函数y=2sin(ωx＋θ)为偶函数(0＜θ＜π)，其图象与直线y=2的交点的横坐标为，若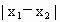的最小值为π，则ω的值为2，θ的值为；

C.函数y=f(x)的图象与直线x=a至多有一个交点；

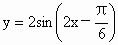D.函数的图象的一个对称点是．

其中正确命题的代号是________(按照原顺序把你认为正确命题的代号都填上)．

给出下列命题：
①函数y=f（x-2）与函数y=f（2-x）的图象关于x=2对称；
②函数y=f（x）导函数为y=f′（x），若f′（x₀）=0，则f（x₀）必为函数y=f（x）的极值；
③函数y=sinx在一象限单调递增；
④y=tanx在其定义域内为单调增函数．
其中正确的命题序号为________．

给出下列命题：
①函数y=f（x-2）与函数y=f（2-x）的图象关于x=2对称；
②函数y=f（x）导函数为y=f′（x），若f′（x）=0，则f（x）必为函数y=f（x）的极值；
③函数y=sinx在一象限单调递增；
④y=tanx在其定义域内为单调增函数．
其中正确的命题序号为．