题目内容
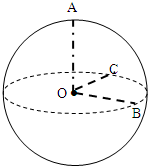 半径为1的球面上有A,B,C三点,其中A和B的球面距离,A和C的球面距离都是
半径为1的球面上有A,B,C三点,其中A和B的球面距离,A和C的球面距离都是| π |
| 2 |
| π |
| 3 |
(1)求球心O到平面ABC的距离;
(2)求异面直线OA和BC的距离;
(3)求二面角B-AC-O的大小.
分析:(1)由已知A和B的球面距离,A和C的球面距离都是
,B和C的球面距离是
,我们可以得到AO⊥面BOC,求出三棱锥O-ABC的体积及三角形ABC的面积,即可求出球心O到平面ABC的距离;
(2)过O作OD⊥BC,可证得OD为异面直线OA和BC的公垂线段,即为异面直线OA和BC的距离,解△OBC,即可得到OD的长,进而得到异面直线OA和BC的距离;
(3)过B作BE⊥OC,可证得BE⊥面AOC,则△ABC在面AOC内的投影为△AEC,则S△ABC•cosθ=S△AEC(其中θ为二面角B-AC-O的大小),分别求出两个三角形的面积,即可求出二面角B-AC-O的大小.
| π |
| 2 |
| π |
| 3 |
(2)过O作OD⊥BC,可证得OD为异面直线OA和BC的公垂线段,即为异面直线OA和BC的距离,解△OBC,即可得到OD的长,进而得到异面直线OA和BC的距离;
(3)过B作BE⊥OC,可证得BE⊥面AOC,则△ABC在面AOC内的投影为△AEC,则S△ABC•cosθ=S△AEC(其中θ为二面角B-AC-O的大小),分别求出两个三角形的面积,即可求出二面角B-AC-O的大小.
解答:解:(1)由题意知:∠AOC=
,∠AOB=
,∠BOC=
,∴AO⊥面BOC
∵OA=OB=OC=1,∴AB=AC=
,BC=1.
∵VA-OBC=
S△OBC|AO|=
又VA-OBC=
S△ABC•h(h为O到平面ABC的距离)
∵S△ABC=
∴h=
∴球心O到平面ABC的距离
(4分)
(2)过O作OD⊥BC,∵AO⊥面BOC,且OD?面BOC,∴OD⊥AO,
∴OD为异面直线OA和BC的公垂线段,即为异面直线OA和BC的距离.
又∵△OBC为等边三角形,且边长为1.所以OD=
异面直线OA和BC的距离为
(8分)
(3)过B作BE⊥OC,∵△BOC为等边三角形,∴则垂足为OC的中点.
∵AO⊥面BOC且BE?面BOC,
∴AO⊥BE,又,BE⊥OC,OA∩OC=O.∴BE⊥面AOC
∴△ABC在面AOC内的投影为△AEC
∵S△ABC•cosθ=S△AEC(其中θ为二面角B-AC-O的大小)S△ABC=
,S△AEC=
∴cosθ=
∴二面角B-AC-O的大小:arccos
(12分)
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
∵OA=OB=OC=1,∴AB=AC=
| 2 |
∵VA-OBC=
| 1 |
| 3 |
| ||
| 12 |
又VA-OBC=
| 1 |
| 3 |
∵S△ABC=
| ||
| 4 |
| ||
| 7 |
∴球心O到平面ABC的距离
| ||
| 7 |
(2)过O作OD⊥BC,∵AO⊥面BOC,且OD?面BOC,∴OD⊥AO,
∴OD为异面直线OA和BC的公垂线段,即为异面直线OA和BC的距离.
又∵△OBC为等边三角形,且边长为1.所以OD=
| ||
| 2 |
异面直线OA和BC的距离为
| ||
| 2 |
(3)过B作BE⊥OC,∵△BOC为等边三角形,∴则垂足为OC的中点.
∵AO⊥面BOC且BE?面BOC,
∴AO⊥BE,又,BE⊥OC,OA∩OC=O.∴BE⊥面AOC
∴△ABC在面AOC内的投影为△AEC
∵S△ABC•cosθ=S△AEC(其中θ为二面角B-AC-O的大小)S△ABC=
| ||
| 4 |
| 1 |
| 4 |
| ||
| 7 |
∴二面角B-AC-O的大小:arccos
| ||
| 7 |
点评:本题考查的知识点是二面角的平面角及求法,空间点到平面的距离及异面直线的距离,(1)中问题常用体积来进行解答,即求出棱锥的体积及底面积,代入得到顶点到底面的距离,(2)的关键是找到公垂线段,(3)的关键是得到BE⊥面AOC,进而得到△ABC在面AOC内的投影为△AEC,并根据S△ABC•cosθ=S△AEC得到答案.

练习册系列答案
相关题目