题目内容
若实数x,y满足不等式组
,且x+y的最小值为-1,则实数m的值是( )
|
分析:根据不等式组作出可行域的大致区域,然后根据目标函数z=x+y取最小值找出最优解,把最优解点的坐标带入目标函数即可求得m的值.
解答:解:令z=x+y,x+y的最小值为-1,指的是函数y=-x+z在y轴上截距的最小值是-1,
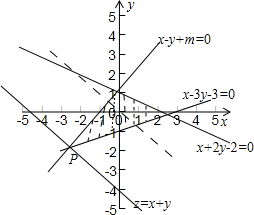
分析不等式组表示的平面区域如图,由图可知,只有目标函数对应的直线经过直线x-3y-3=0与x-y+m=0的交点时,
z=x+y取最小值,联立两直线方程解得交点P(-
m-
,-
m-
),所以-1=-
m-
-
m-
,解得:m=-1.
故选B.
分析不等式组表示的平面区域如图,由图可知,只有目标函数对应的直线经过直线x-3y-3=0与x-y+m=0的交点时,
z=x+y取最小值,联立两直线方程解得交点P(-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选B.

点评:本题考查了简单的线性规划,考查了学生的作图能力,找二元一次不等式表示的平面区域可采用取特殊点的办法,解答此题的关键是找到最优解,是中低档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 . ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 . ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 . ,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时,
,且对于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立.又函数y=f(x-1)的图象关于点(1,0)对称,则当 1≤x≤4时, 的取值范围为 .
的取值范围为 .