Question

定义在R上的函数y=f（x），若对任意不等实数x₁，x₂满足

f(x1)-f(x2)

x1-x2

＜0，且对于任意的x，y∈R，不等式f（x²-2x）+f（2y-y²）≤0成立．又函数y=f（x-1）的图象关于点（1，0）对称，则当 1≤x≤4时，

y

x

的取值范围为

[-

1

2

，1]

．

Answer 1

分析：由

f(x1)-f(x2)

x1-x2

＜0可得：函数f（x）是递减函数．由函数y=f（x-1）的图象关于点（1，0）对称，可得函数f（x）是奇函数，再结合f（x²-2x）+f（2y-y²）≤0可得（x-y）（x+y-2）≥0（1≤x≤4），进而利用线性规划的知识解决问题．

解答：解：因为对任意不等实数x₁，x₂满足

f(x1)-f(x2)

x1-x2

＜0，
所以函数f（x）是定义在R上的单调递减函数．
因为函数y=f（x-1）的图象关于点（1，0）对称，
所以函数y=f（x）的图象关于点（0，0）对称，即函数f（x）是定义在R上的奇函数．
又因为对于任意的x，y∈R，不等式f（x²-2x）+f（2y-y²）≤0成立，
所以f（x²-2x）≥f（-2y+y²）成立，
所以根据函数的单调性可得：对于任意的x，y∈R，不等式x²-2x≥y²-2y成立，即（x-y）（x+y-2）≥0（1≤x≤4），
所以可得其可行域，如图所示：

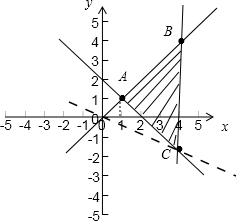
因为

y

x

=

y-0

x-0

，
所以

y

x

表示点（x，y）与点（0，0）连线的斜率，
所以结合图象可得：

y

x

的最小值是直线OC的斜率-

1

2

，最大值是直线AB的斜率1，
所以

y

x

的范围为：[-

1

2

，1]．
故答案为：[-

1

2

，1]．

点评：解决此类问题的关键是熟练掌握抽象函数的性质的证明与判断，如单调性、奇偶性的证明与判断，并且熟练的利用函数的性质解有关的不等式，以及熟练掌握线性规划问题，此题综合性较强知识点也比较零散，对学生掌握知识与运用知识的能力有一定的要求．