题目内容
已知点A(4,4)在抛物线y2=px(p>0)上,该抛物线的焦点为F,过点A作直线l:x=-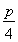
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
【答案】
x-2y+4=0
【解析】点A在抛物线上,所以16=4p,所以p=4,所以抛物线的焦点为F(1,0),准线方程为x=-1,垂足M(-1,4),由抛物线的定义得|AF|=|AM|,所以∠MAF的平分线所在的直线就是线段MF的垂直平分线,kMF=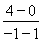
=-2,所以∠MAF的平分线所在的直线方程为y-4=
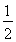(x-4),即x-2y+4=0.
练习册系列答案
相关题目
,-2) B.(4,
) C.(6-4
,4
-2) D.(4,4
)
,-2) B.(4,
) C.(6-4
＝1的右焦点重合，该抛物线上有一点M，它在y轴上的射影为N，则|MA|＋|MN|的最小值为___________
＝1的右焦点重合，该抛物线上有一点M，它在y轴上的射影为N，则|MA|＋|MN|的最小值为___________。