题目内容
已知点P（1，
）是曲线f（x）=Asin（ωx+φ）（A＞0，ω＞0|φ|＜
）的一个最高点，且f（9-x）=f（9+x），曲线区间（1，9）内与x轴有唯一一个交点，求这个函数的解析式，并作出一个周期的图象．
| 3 |
| π |
| 2 |
分析：根据点P（1，
）是曲线f（x）=Asin（ωx+φ）（A＞0，ω＞0|φ|＜
）的一个最高点，可知A=
，由f（9-x）=f（9+x）得函数的一条对称轴方程为x=9，根据曲线区间（1，9）内与x轴有唯一一个交点，可知函数的周期，因此可求得函数的解析式；利用五点法列表，描点，即可画出函数的图象．
| 3 |
| π |
| 2 |
| 3 |
解答：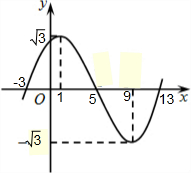
解：∵点P（1，
）是曲线f（x）=Asin（ωx+φ）（A＞0，ω＞0|φ|＜
）的一个最高点，
∴A=
，
∵f（9-x）=f（9+x），曲线区间（1，9）内与x轴有唯一一个交点，
∴x=9是曲线的一条对称轴，且
=8
∴T=16，
而T=
，ω=
，
+φ=
+2kπ，k∈Z，
∴φ=
+2kπ，k∈Z，∵|φ|＜
，
φ=
∴f（x）=
sin（
x+
），
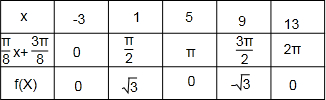其图象如图所示：
解：∵点P（1，| 3 |
| π |
| 2 |
∴A=
| 3 |
∵f（9-x）=f（9+x），曲线区间（1，9）内与x轴有唯一一个交点，
∴x=9是曲线的一条对称轴，且
| T |
| 2 |
∴T=16，
而T=
| 2π |
| ω |
| π |
| 8 |
| π |
| 8 |
| π |
| 2 |
∴φ=
| 3π |
| 8 |
| π |
| 2 |
φ=
| 3π |
| 8 |
∴f（x）=
| 3 |
| π |
| 8 |
| 3π |
| 8 |
其图象如图所示：点评：本题考查y=Asin（ωx+φ）的解析式的求法以及五点法作图，根据题意求出周期是解题的关键，考查运算能力和作图能力，属中档题．
练习册系列答案
相关题目
与向量、圆交汇．例5：已知F1、F2分别为椭圆C1：