题目内容
已知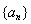 是等差数列,首项
是等差数列,首项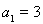 ,前
,前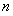 项和为
项和为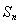 .令
.令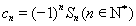 ,
,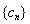 的前
的前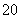 项和
项和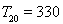 .数列
.数列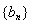 是公比为
是公比为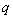 的等比数列,前
的等比数列,前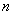 项和为
项和为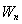 ,且
,且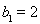 ,
,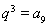 .
.
(1)求数列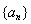 、
、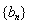 的通项公式;
的通项公式;
(2)证明: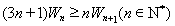 .
.
【答案】
(1) 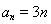 ,
,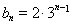 ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)首先设等差数列的公差为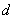 ,由已知建立
,由已知建立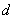 的方程,求得
的方程,求得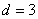 ,写出等差数列的通项公式;进一步确定等比数列的公比,求得等比数列的通项公式.
,写出等差数列的通项公式;进一步确定等比数列的公比,求得等比数列的通项公式.
(2)求得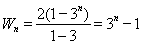 ,将不等式加以转化成
,将不等式加以转化成 ,
,
即证: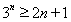 .注意到这是与自然数有关的不等式证明问题,故考虑应用数学归纳法.
.注意到这是与自然数有关的不等式证明问题,故考虑应用数学归纳法.
很明显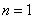 时,
时,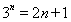 ,因此用数学归纳法证明:当
,因此用数学归纳法证明:当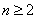 时,
时,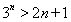 .
.
试题解析:(1)设等差数列的公差为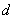 ,因为
,因为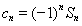
所以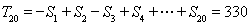
则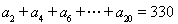
则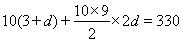
解得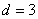 ,所以
,所以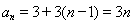 4分
4分
所以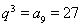 ,
,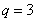
所以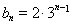 6分
6分
(2)由(1)知,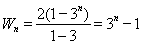
要证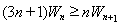 ,
,
只需证
即证: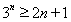 8分
8分
当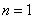 时,
时,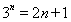
下面用数学归纳法证明:当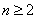 时,
时,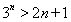
(1)当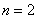 时,左边
时,左边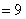 ,右边
,右边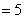 ,左
,左 右,不等式成立
右,不等式成立
(2)假设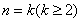 ,
,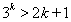
则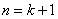 时,
时,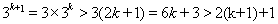
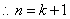 时不等式成立
时不等式成立
根据(1)(2)可知:当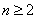 时,
时,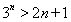
综上可知: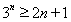 对于
对于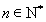 成立
成立
所以 12分
12分
考点:等差数列、等比数列的通项公式及其求和公式,数学归纳法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目