题目内容
求下列函数的最值(1)x>0时,求
 的最小值.
的最小值.(2)设
 ,求
,求 的最大值.
的最大值.(3)若0<x<1,求y=x4(1-x2)的最大值.
(4)若a>b>0,求
 的最小值.
的最小值.
【答案】分析:(1)本题可为三个数的和,将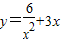 变为
变为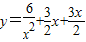 ,用基本不等式求出最小值.
,用基本不等式求出最小值.
(2)将函数变形f(x)=(log3x-3)(log3x+1)=(log3x)2-2log3x-3,令log3x=t,转化为二次函数解决.
(3)将原函数式化为y=x4(1-x2)=4× x2•
x2• x2(1-x2)后利用基本不等式求解即可.
x2(1-x2)后利用基本不等式求解即可.
(4)本题可为三个数的和,可进行变形a+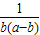 =a-b+b+
=a-b+b+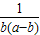 用基本不等式求出最小值.
用基本不等式求出最小值.
解答:解:(1)y=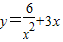 ,
,
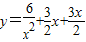
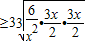 =9,
=9,
当且仅当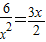 时,取等号,
时,取等号,
∴函数的最小值为9.
(2)f(x)=(log3x-3)(log3x+1)=(log3x)2-2log3x-3
令log3x=t,由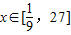 ,得,t∈[-2,3]
,得,t∈[-2,3]
∴y=t2-2t-3,t∈[-2,3]
当t=-2或3时,ymax=5
(3)y=x4(1-x2)=4× x2•
x2• x2(1-x2)
x2(1-x2)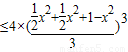 =
=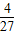 ,
,
故y=x4(1-x2)的最大值是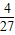 .
.
(4)∵a>b>0
a+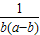 =a-b+b+
=a-b+b+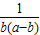 ≥3=3
≥3=3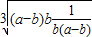 =3,
=3,
当且仅当a-b=b=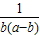 时取等号.
时取等号.
故最大值为:3.
点评:本题考查基本不等式公式,此题主要考查求函数最值问题,在做题的时候不能只考虑研究函数图象的方式求最值,需要多分析题目,对于特殊的函数可以用基本不等式直接求得最值.
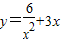 变为
变为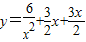 ,用基本不等式求出最小值.
,用基本不等式求出最小值.(2)将函数变形f(x)=(log3x-3)(log3x+1)=(log3x)2-2log3x-3,令log3x=t,转化为二次函数解决.
(3)将原函数式化为y=x4(1-x2)=4×
 x2•
x2• x2(1-x2)后利用基本不等式求解即可.
x2(1-x2)后利用基本不等式求解即可.(4)本题可为三个数的和,可进行变形a+
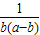 =a-b+b+
=a-b+b+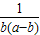 用基本不等式求出最小值.
用基本不等式求出最小值.解答:解:(1)y=
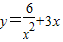 ,
,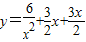
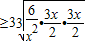 =9,
=9,当且仅当
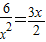 时,取等号,
时,取等号,∴函数的最小值为9.
(2)f(x)=(log3x-3)(log3x+1)=(log3x)2-2log3x-3
令log3x=t,由
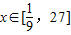 ,得,t∈[-2,3]
,得,t∈[-2,3]∴y=t2-2t-3,t∈[-2,3]
当t=-2或3时,ymax=5
(3)y=x4(1-x2)=4×
 x2•
x2• x2(1-x2)
x2(1-x2)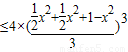 =
=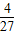 ,
,故y=x4(1-x2)的最大值是
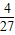 .
.(4)∵a>b>0
a+
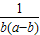 =a-b+b+
=a-b+b+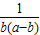 ≥3=3
≥3=3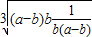 =3,
=3,当且仅当a-b=b=
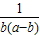 时取等号.
时取等号.故最大值为:3.
点评:本题考查基本不等式公式,此题主要考查求函数最值问题,在做题的时候不能只考虑研究函数图象的方式求最值,需要多分析题目,对于特殊的函数可以用基本不等式直接求得最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目