题目内容
在△ABC中，sinA∶sinB∶sinC＝3∶2∶4，则cosC的值为 .
－
；
解析试题分析：由题意利用正弦定理，推出a，b，c的关系，然后利用余弦定理求出cosB的值．解：△ABC的内角A，B，C满足6sinA=4sinB=3sinC，所以6a=4b=3c，不妨令a=3，b=2，c=4，所以由余弦定理：c2=a2+b2-2abcosB，所以cosB=－，故填写－。
考点：正弦定理，余弦定理
点评：本题是基础题，考查正弦定理，余弦定理的应用，考查计算能力，常考题型．
练习册系列答案
阅读快车系列答案
相关题目
中，若
，
，则
的最大值为__________．
与两灯塔
、
的距离分别为300米和500米，测得灯塔
，灯塔
，
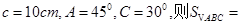
中.若b=5，
，sinA=
，则a=___________________.
中，
所对的边分别是
，若
，且
，则
= 或 ．
，则边长
的取值范围是_________
中，角A、B、C所对的边分别为
、
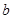、，若
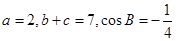，则
.
的三边的长是3个连续的自然数，其中最大角为
，则
＝_____