题目内容
以下有关线性回归分析的说法不正确的是
A.通过最小二乘法得到的线性回归直线经过样本的中心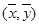 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.相关系数r越小,表明两个变量相关性越弱 |
D. 越接近1,表明回归的效果越好 越接近1,表明回归的效果越好 |
C
解析试题分析:对于A.通过最小二乘法得到的线性回归直线经过样本的中心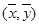 ,显然成立。
,显然成立。
对于B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值,符合定义。
最小的a,b的值,符合定义。
对于C.相关系数r越小,表明两个变量相关性越弱,应该是绝对值越小,相关性越弱,故错误。
对于D. 越接近1,表明回归的效果越好,成立,故选C.
越接近1,表明回归的效果越好,成立,故选C.
考点:线性回归方程
点评:解决的关键是利用最小二乘法来求解回归的效果,属于基础题。

练习册系列答案
相关题目
右表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是 ,则a等于( ).
,则a等于( ).
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 5.5 | 5 | 4 | 3.5 |
设有一个回归方程为y=2-3x,变量x增加1个单位时,则y平均( )
| A.增加2个单位 | B.减少2个单位 | C.增加3个单位 | D.减少3个单位 |
工人月工资(元)依劳动产值(千元)变化的回归直线方程为 =60+90x,下列判断正确的是( )
=60+90x,下列判断正确的是( )
| A.劳动产值为1 000元时,工资为50元 |
| B.劳动产值提高1 000元时,工资提高150元 |
| C.劳动产值提高1 000元时,工资提高90元 |
| D.劳动产值为1 000元时,工资为90元 |
在如下图所示的各图中,两个变量具有相关关系的是( )
| A.(1)(2) | B.(1)(3) |
| C.(2)(4) | D.(2)(3) |
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为( )
| A.45,75,15 | B.45,45,45 |
| C.30,90,15 | D.45,60,30 |
从总数为N的一批零件中抽取一个容量为30的样本,若每个零件被抽取的可能性为25%,则N为( )
| A.150 | B.200 | C.100 | D.120 |
图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( )
| A.31,26 | B.36,23 |
| C.36,26 | D.31,23 |