题目内容

19．已知等腰直角三角形的直角边的长为2，将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的表面积为4$\sqrt{2}$π．

分析 画出满足条件的几何体，根据圆锥的侧面积公式直接计算即可得到答案

解答 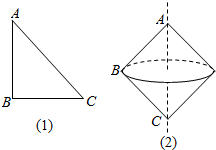解：如图为等腰直角三角形旋转而成的旋转体．
这是两个底面半径为$\sqrt{2}$，母线长2的圆锥，
故S=2πrl=2π×$\frac{\sqrt{2}}{2}$×2=4$\sqrt{2}$π．
故答案为：4$\sqrt{2}$π．

点评 本题考查圆锥的侧面积公式，考查空间想象能力以及计算能力．是基础题．

练习册系列答案
相关题目
9．函数f（x）=$\frac{\sqrt{x-1}}{x}$的值域是$[0，\frac{1}{2}]$．
10．求下列各式的值．
（1）${（{\frac{9}{4}}）^{\frac{1}{2}}}+（9.6{）^0}-{（{\frac{8}{27}}）^{-\frac{1}{3}}}$；
（2）log28+lg25+lg4．
7．已知f（x+1）=x2，则f（3）=（　　）
A．9B．16C．4D．-4
14．函数$y=\frac{{\sqrt{{x^2}-1}}}{x-1}$的定义域是（　　）
A．{x|-1≤x＜1}B．{x|x≤-1或x＞1}C．{x|-1≤x≤1}D．{x|x≤-1或x≥1}
4．已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）求函数y=f（x）的单调增区间；
（Ⅲ）当x∈[-$\frac{π}{12}$，$\frac{π}{2}$]，求f（x）的值域．
11．若向量$\overrightarrow a=（{1，0，z}）$与向量$\overrightarrow b=（{2，1，2}）$的夹角的余弦值为$\frac{2}{3}$，则z=0，$|{\overrightarrow a-2\overrightarrow b}|$=$\sqrt{29}$．
8．已知数列{an}中，a1=$\frac{1}{2}$，an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$（n∈N*）．
（I）证明数列{$\frac{1}{{a}_{n}}$}为等差数列，并求数列{an}的通项公式；
（Ⅱ）已知数列{bn}的前n项和为Sn，且对任意正整数n，都有（1+$\frac{{b}_{n}}{{{a}^{2}}_{n}}$）•n=$\frac{5{n}^{2}+10n+9}{4n+4}$成立，证明：$\frac{1}{2}$≤Sn＜1．
9．两个变量x，y的散点图与函数y=axb的图象近似，将函数y=axb作线性变换，再利用最小二乘法得到的回归方程为u=3+0.5v，若x=e2，则y的近似值为（　　）
A．eB．e2C．e3D．e4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网