题目内容
已知点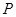 在曲线
在曲线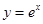 上,点
上,点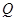 在曲线
在曲线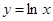 上,则
上,则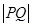 的最小值是
的最小值是

解析试题分析:∵曲线y=ex(e自然对数的底数)与曲线y=lnx互为反函数,其图象关于y=x对称,则对于求解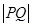 的最小值问题,故可先求点P到直线y=x的最近距离d,设曲线y=ex上斜率为1的切线为y=x+b,∵y′=ex,由ex=1,得x=0,故切点坐标为(0,1),即b=1,∴d=
的最小值问题,故可先求点P到直线y=x的最近距离d,设曲线y=ex上斜率为1的切线为y=x+b,∵y′=ex,由ex=1,得x=0,故切点坐标为(0,1),即b=1,∴d= ,∴丨PQ丨的最小值为2d=
,∴丨PQ丨的最小值为2d= 。
。
考点:本题主要考查了互为反函数的函数图象的对称性,导数的几何意义,曲线的切线方程的求法,转化化归的思想方法
点评:考虑到两曲线关于直线y=x对称,求丨PQ丨的最小值可转化为求P到直线y=x的最小距离,再利用导数的几何意义,求曲线上斜率为1的切线方程,从而得此距离。

练习册系列答案
相关题目
函数 的实数解落在的区间是( )
的实数解落在的区间是( )
A.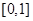 | B.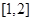 | C. | D.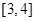 |
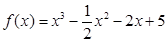 ,当
,当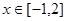 时,
时,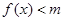 恒成立,则实数
恒成立,则实数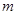 的取值范围为 .
的取值范围为 . 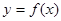 在点P处的切线方程是
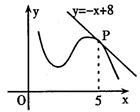
在点P处的切线方程是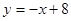 ,则
,则 =
= 
 ,若
,若 ,则
,则 .
. 的值为 .
的值为 .  与
与 轴及直线
轴及直线 围成的图形面积为
围成的图形面积为 ,则m的值为 .
,则m的值为 .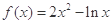 在其定义域内的一个子区间
在其定义域内的一个子区间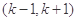 内不是单调函数,则实数
内不是单调函数,则实数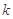 的取值范围是
的取值范围是