题目内容
本小题满分14分
已知：数列
，
中，
,
，且当
时，
，
，
成等差数列，
，
，
成等比数列.
（1）求数列，的通项公式；
（2）求最小自然数
，使得当
时，对任意实数
，不等式
≥
恒成立；
（3）设
（），求证：当
都有
.
【解】（1）依题意2
=
+
,
=
.又∵
，
，∴≥0，≥0 , 且
,∴
（
≥2）, ∴数列
是等差数列，又
,∴
,
也适合.∴
，
. ………………4分
(2) 将，代入不等式
≥
（
）
整理得：
≥0 ………………………6分
令
，则是关于
的一次函数，由题意可得
， ∴
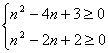，解得
≤1或≥3. ∴存在最小自然数
，使得当≥
时，不等式（）恒成立. …………8分
练习册系列答案
备战中考寒假系列答案
相关题目
：“函数
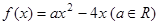在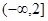
上单调递减”，命题
：“
，
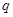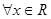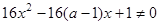”，若命题“
的取值范围。k*s5u
，
，当
时，
恒成立，试求m的取值范围。
为平面上点
的坐标．
，从集合
中随机取一个数作为
，从集合
中随机取一个数作为
，求点
，求点
所表示的平面区域内的概率．
}的前n项和为
，满足
}是等比数列.并求数列{
}满足
为数列
的前n项和，求