题目内容
已知数列{an}满足3an+1+an=0,a2=-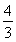 ,则{an}的前10项和为________.
,则{an}的前10项和为________.
3(1-3-10)
【解析】q=-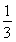 ,a1=4,则S10=
,a1=4,则S10= =3(1-3-10).
=3(1-3-10).

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
题目内容
已知数列{an}满足3an+1+an=0,a2=-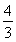 ,则{an}的前10项和为________.
,则{an}的前10项和为________.
3(1-3-10)
【解析】q=-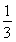 ,a1=4,则S10=
,a1=4,则S10= =3(1-3-10).
=3(1-3-10).

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案