题目内容
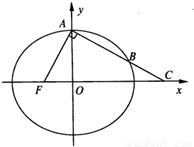
如图,椭圆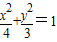 的左焦点为F,上顶点为A,过点A作直线AF的垂线分别交椭圆、x轴于B,C两点.
的左焦点为F,上顶点为A,过点A作直线AF的垂线分别交椭圆、x轴于B,C两点.(1)若
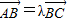 ,求实数λ的值;
,求实数λ的值;(2)设点P为△ACF的外接圆上的任意一点,当△PAB的面积最大时,求点P的坐标.
【答案】分析:(1)由已知条件可得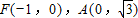 ,
, .利用两直线垂直的关系可求直线AB的方程,及C的坐标,联立直线AB与椭圆的方程可求B,利用向量的坐标表示可求 λ的值
.利用两直线垂直的关系可求直线AB的方程,及C的坐标,联立直线AB与椭圆的方程可求B,利用向量的坐标表示可求 λ的值
(2)由已知可得△ACF的外接圆的圆心为D(1,0),半径为2.从而可得圆D的方程为(x-1)2+y2=4.AB为定值,要求△PAB的面积最大时,转化为求点P到直线AC的距离最大.利用圆的知识求解即可
解答: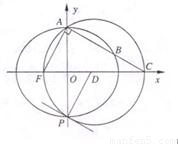 解:(1)由条件得
解:(1)由条件得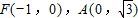 ,
, .
.
因为AB⊥AF,
所以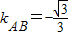 ,
,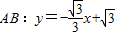 .
.
令y=0,得x=3,
所以点C的坐标为(3,0).
由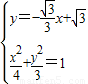 得13x2-24x=0,解得x1=0(舍)
得13x2-24x=0,解得x1=0(舍)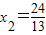 .
.
所以点B的坐标为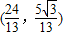 .
.
因为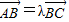 ,所以λ>0,且
,所以λ>0,且 .
.
(2)因为△ACF是直角三角形,
所以△ACF的外接圆的圆心为D(1,0),半径为2.
所以圆D的方程为(x-1)2+y2=4.
因为AB为定值,
所以当△PAB的面积最大时,点P到直线AC的距离最大.
过D作直线AC的垂线m,则点P为直线m与圆D的交点.
直线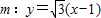 与(x-1)2+y2=4联立得x=2(舍)或x=0,
与(x-1)2+y2=4联立得x=2(舍)或x=0,
所以点P的坐标为(0,-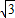 )
)
点评:本题主要考查了椭圆的基本概念,直线垂直关系的应用,向量共线的坐标表示,直线与椭圆的相交关系,及圆的知识的综合应用,试题的运算较多,考查了运算的能力.
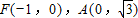 ,
,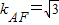 .利用两直线垂直的关系可求直线AB的方程,及C的坐标,联立直线AB与椭圆的方程可求B,利用向量的坐标表示可求 λ的值
.利用两直线垂直的关系可求直线AB的方程,及C的坐标,联立直线AB与椭圆的方程可求B,利用向量的坐标表示可求 λ的值(2)由已知可得△ACF的外接圆的圆心为D(1,0),半径为2.从而可得圆D的方程为(x-1)2+y2=4.AB为定值,要求△PAB的面积最大时,转化为求点P到直线AC的距离最大.利用圆的知识求解即可
解答:
 解:(1)由条件得
解:(1)由条件得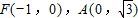 ,
,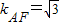 .
.因为AB⊥AF,
所以
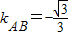 ,
,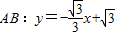 .
.令y=0,得x=3,
所以点C的坐标为(3,0).
由
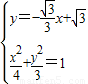 得13x2-24x=0,解得x1=0(舍)
得13x2-24x=0,解得x1=0(舍)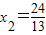 .
.所以点B的坐标为
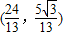 .
.因为
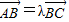 ,所以λ>0,且
,所以λ>0,且 .
.(2)因为△ACF是直角三角形,
所以△ACF的外接圆的圆心为D(1,0),半径为2.
所以圆D的方程为(x-1)2+y2=4.
因为AB为定值,
所以当△PAB的面积最大时,点P到直线AC的距离最大.
过D作直线AC的垂线m,则点P为直线m与圆D的交点.
直线
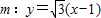 与(x-1)2+y2=4联立得x=2(舍)或x=0,
与(x-1)2+y2=4联立得x=2(舍)或x=0,所以点P的坐标为(0,-
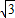 )
)点评:本题主要考查了椭圆的基本概念,直线垂直关系的应用,向量共线的坐标表示,直线与椭圆的相交关系,及圆的知识的综合应用,试题的运算较多,考查了运算的能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
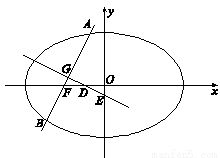
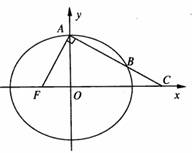 如图,椭圆
如图,椭圆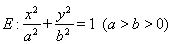
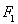
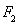
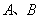
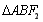
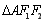
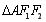

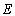
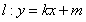
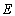
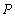
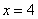
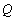
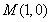
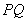
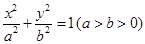 的左焦点为
的左焦点为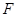 ,过点
,过点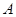 ,
,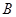 两点.当直线
两点.当直线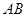 经过椭圆的一个顶点时,其倾斜角恰为
经过椭圆的一个顶点时,其倾斜角恰为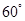 .
.
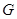 ,
,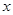 轴和
轴和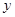 轴分别交于
轴分别交于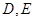 两点,
两点,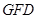 的面积为
的面积为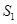 ,△
,△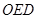 (
(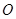 为原点)的面积为
为原点)的面积为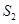 ,求
,求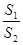 的取值范围.
的取值范围. 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.