题目内容
【题目】选修4-4:坐标系与参数方程
将圆![]() 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线![]() .
.
(1)写出曲线![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别为曲线
分别为曲线![]() 和直线
和直线![]() 上的一点,求
上的一点,求![]() 的最近距离.
的最近距离.
【答案】(1) ![]() (
(![]() 为参数);(2)
为参数);(2)![]() .
.
【解析】
试题分析:(1)设![]() 为圆上一点,在已知变换下
为圆上一点,在已知变换下![]() 上的点
上的点![]() ,得出椭圆的标准方程,进而得出椭圆的参数方程;(2)得出直线的方程,设
,得出椭圆的标准方程,进而得出椭圆的参数方程;(2)得出直线的方程,设![]() ,利用点到直线的距离公式,求得
,利用点到直线的距离公式,求得![]() ,利用三角函数的性质,即可求解最小值.
,利用三角函数的性质,即可求解最小值.
试题解析:(1)设![]() 为圆上一点,在已知变换下
为圆上一点,在已知变换下![]() 上的点
上的点![]() ,依题意
,依题意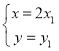 ,
,
由![]() 得
得![]() ,即
,即![]() ,
,
故![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)
为参数)
(2)将![]() 的极坐标方程化为直角坐标方程:
的极坐标方程化为直角坐标方程:![]() ,
,
设![]() ,设点
,设点![]() 到
到![]() 的距离为
的距离为![]() ,
,
![]() ,
,
其中![]() ,取等时
,取等时![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 8 | 0.16 |
149.5~153.5 | 6 | 0.12 |
153.5~157.5 | 14 | 0.28 |
157.5~161.5 | 10 | 0.20 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 |
|
|
合计 |
|
|
(1)求出表中字母![]() 所对应的数值;
所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5![]() 范围内有多少人?
范围内有多少人?

