题目内容
已知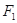 ,
,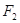 分别是椭圆
分别是椭圆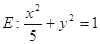 的左、右焦点
的左、右焦点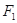 ,
,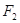 关于直线
关于直线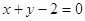 的对称点是圆
的对称点是圆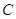 的一条直径的两个端点.
的一条直径的两个端点.
(Ⅰ)求圆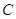 的方程;
的方程;
(Ⅱ)设过点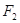 的直线
的直线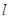 被椭圆
被椭圆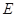 和圆
和圆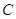 所截得的弦长分别为
所截得的弦长分别为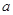 ,
,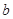 .当
.当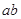 最大时,求直线
最大时,求直线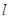 的方程.
的方程.
(Ⅰ)圆 的方程为
的方程为 ;(Ⅱ)直线的方程是
;(Ⅱ)直线的方程是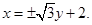
解析试题分析:(Ⅰ)求圆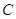 的方程,圆
的方程,圆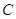 的直径为
的直径为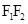 ,它的圆心为
,它的圆心为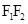 的中点关于直线
的中点关于直线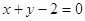 的对称点,故本题先求出
的对称点,故本题先求出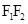 的长,从而得半径
的长,从而得半径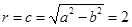 ,
,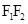 的中点
的中点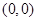 ,只需求出它关于直线
,只需求出它关于直线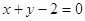 的对称点,求点关于线对称的方法为:两点连线垂直对称轴,两点的中点在对称轴上,这样求出圆心
的对称点,求点关于线对称的方法为:两点连线垂直对称轴,两点的中点在对称轴上,这样求出圆心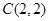 ,从而可以写出圆的方程;(Ⅱ)设过点
,从而可以写出圆的方程;(Ⅱ)设过点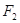 的直线
的直线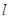 被椭圆
被椭圆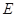 和圆
和圆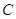 所截得的弦长分别为
所截得的弦长分别为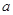 ,
,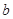 .当
.当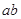 最大时,求直线
最大时,求直线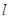 的方程,这是直线与二次曲线的位置关系问题,可采用设而不求的方法来解,设直线
的方程,这是直线与二次曲线的位置关系问题,可采用设而不求的方法来解,设直线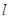 方程为:
方程为: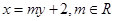 ,设直线与椭圆相交与点
,设直线与椭圆相交与点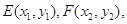 利用弦长公式求出
利用弦长公式求出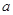 的值,根据圆的性质求出
的值,根据圆的性质求出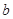 的值,从而得
的值,从而得 ,可用基本不等式确定最大值时的
,可用基本不等式确定最大值时的 的值,就得直线方程.
的值,就得直线方程.
试题解析:(Ⅰ) 设圆 和圆
和圆 关于直线
关于直线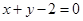 对称,由题意知圆
对称,由题意知圆 的直径为
的直径为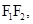 所以圆心
所以圆心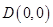 ,半径
,半径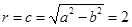 ,圆心
,圆心 与圆心
与圆心 关于直线
关于直线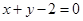 对称
对称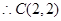 ,故圆
,故圆 的方程为
的方程为 ;
;
(Ⅱ)由(Ⅰ)知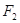 (2,0), 设直线
(2,0), 设直线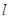 方程为:
方程为: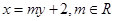 ,
, 圆心
圆心 到直线
到直线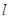 的距离
的距离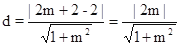 ,由垂径定理和勾股定理得:
,由垂径定理和勾股定理得: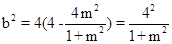 . 设直线与椭圆相交与点
. 设直线与椭圆相交与点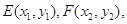 由
由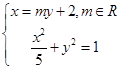 得:
得: 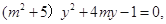 由韦达定理可得:
由韦达定理可得: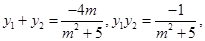 依题意可知:
依题意可知: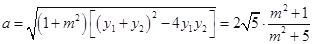
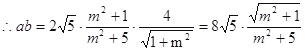 ,令
,令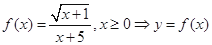 在
在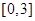 单调递增,在
单调递增,在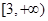 单调递减,
单调递减,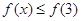
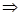 当
当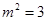 时,
时,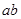 取得最大值,此时直线的方程是
取得最大值,此时直线的方程是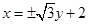 ,所以当
,所以当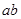 取得最大值时,直线的方程是
取得最大值时,直线的方程是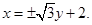
考点:椭圆的方程、圆的方程、直线与椭圆的位置关系、直线的方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 +4-3m=0.
+4-3m=0. 垂直;
垂直; 与
与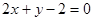 的交点,且平行于直线
的交点,且平行于直线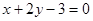 的直线方程.
的直线方程. :
: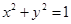 和定点
和定点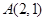 ,由⊙
,由⊙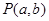 向⊙
向⊙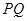 ,切点为
,切点为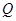 ,且满足
,且满足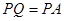 .
. 间满足的等量关系;
间满足的等量关系; 为圆心所作的⊙
为圆心所作的⊙ ,
,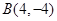 ,
,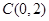 ,
,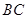 边上的中线所在直线方程;
边上的中线所在直线方程;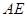 所在直线方程.
所在直线方程.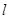 过点P(-2,1),
过点P(-2,1),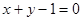 平行,求直线
平行,求直线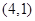 ,B
,B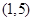 ,C
,C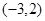 ;
;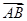 =(4,2).
=(4,2).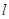 经过直线
经过直线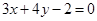 与直线
与直线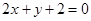 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
. .
.