题目内容
定义在D={x∈R|x≠0}上的函数f(x)满足两个条件:①对于任意x、y∈D,都有f(x)f(y)-f(xy)=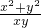 ;②曲线y=f(x)存在与直线x+y+1=0平行的切线.
;②曲线y=f(x)存在与直线x+y+1=0平行的切线.
(Ⅰ)求过点(-1, )的曲线y=f(x)的切线的一般式方程;
)的曲线y=f(x)的切线的一般式方程;
(Ⅱ)当x∈(0,+∞),n∈N+时,求证:fn(x)-f(xn)≥2n-2.
解:(Ⅰ)令x=y=1得,f2(1)-f(1)=2,解得f(1)=-1或f(1)=2.
当f(1)=-1时,令y=1得,f(x)=-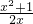 ,即f(x)=-
,即f(x)=- (x+
(x+ ),
),
f′(x)=- (1-
(1-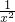 ),
),
由f′(x)=-1得,x2=-1,此方程在D上无解,这说明曲线y=f(x)不存在与直线x+y+1=0平行的切线,不合题意,
则f(1)=2,此时,令y=1得,f(x)=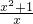 =x+
=x+ ,f′(x)=1-
,f′(x)=1-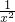 ,
,
由f′(x)=-1得,x2= ,此方程在D上有解,符合题意.
,此方程在D上有解,符合题意.
设过点(-1, )的切线切曲线y=f(x)于(x0,x0+
)的切线切曲线y=f(x)于(x0,x0+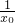 ),则切线的斜率为1-
),则切线的斜率为1-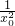 ,
,
其方程为y-x0-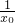 =(1-
=(1-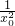 )(x-x0),把点(-1,
)(x-x0),把点(-1, )的坐标代入整理得,
)的坐标代入整理得,
5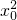 -8x0-4=0,解得x0=-
-8x0-4=0,解得x0=- 或x0=2,
或x0=2,
把x0=- 或x0=2分别代入上述方程得所求的切线方程是:y=-
或x0=2分别代入上述方程得所求的切线方程是:y=-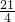 x-5和y=
x-5和y= x+1,
x+1,
即21x+4y+20=0和3x-4y+4=0.
(Ⅱ)由(Ⅰ)知f(x)=x+ ,当n∈N*时,
,当n∈N*时,
fn(x)-f(xn)=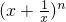 -(xn+
-(xn+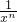 )
)
= xn-1•
xn-1• +
+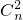 xn-2•
xn-2•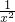 +…+
+…+ x2•
x2• +
+ x•
x•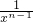
= xn-2+
xn-2+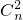 xn-4+…+
xn-4+…+
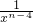 +
+
 ,
,
由x∈(0,+∞),n∈N*知,xn∈(0,+∞),那么
2(fn(x)-f(xn))= xn-2+
xn-2+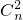 xn-4+…+
xn-4+…+
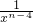 +
+

+
 +
+
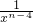 +…+
+…+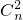 xn-4+
xn-4+ xn-2
xn-2
= xn-2+
xn-2+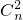 xn-4+…+
xn-4+…+
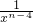 +
+

+
 +
+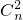
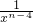 +…+
+…+ xn-4+
xn-4+ xn-2
xn-2
= (xn-2+
(xn-2+ )+
)+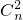 (xn-4+
(xn-4+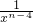 )+…+
)+…+ (xn-2+
(xn-2+ )
)
≥2 +2
+2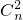 +…+2
+…+2 )
)
=2( +
+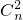 +…+
+…+ )
)
=2[(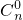 +
+ +
+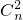 +…+
+…+ +
+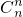 )-
)-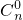 -
-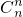 )]
)]
=2(2n-2)
所以fn(x)-f(xn)≥2n-2.
分析:(Ⅰ)令x=y=1,可求得f(1)=2,从而可求得f(x)=x+ ,设过点(-1,
,设过点(-1, )的切线切曲线y=f(x)于(x0,x0+
)的切线切曲线y=f(x)于(x0,x0+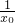 ),则切线的斜率为1-
),则切线的斜率为1-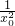 ,于是可求得切线方程,将点(-1,
,于是可求得切线方程,将点(-1, )的坐标代入方程即可求得x0,从而可得过点(-1,
)的坐标代入方程即可求得x0,从而可得过点(-1, )的曲线y=f(x)的切线的一般式方程;
)的曲线y=f(x)的切线的一般式方程;
(Ⅱ)由(Ⅰ)知f(x)=x+ ,当n∈N*时,fn(x)-f(xn)=
,当n∈N*时,fn(x)-f(xn)=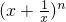 -(xn+
-(xn+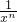 ),利用二项式定理将
),利用二项式定理将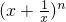 展开,采用倒序相加法可求得2(fn(x)-f(xn)),再利用基本不等式即可证得结论.
展开,采用倒序相加法可求得2(fn(x)-f(xn)),再利用基本不等式即可证得结论.
点评:本题考查利用导数研究曲线上某点切线方程,考查不等式的证明,突出二项式定理及倒序相加法与基本不等式的综合运用,属于难题.
当f(1)=-1时,令y=1得,f(x)=-
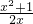 ,即f(x)=-
,即f(x)=- (x+
(x+ ),
),f′(x)=-
 (1-
(1-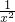 ),
),由f′(x)=-1得,x2=-1,此方程在D上无解,这说明曲线y=f(x)不存在与直线x+y+1=0平行的切线,不合题意,
则f(1)=2,此时,令y=1得,f(x)=
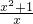 =x+
=x+ ,f′(x)=1-
,f′(x)=1-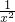 ,
,由f′(x)=-1得,x2=
 ,此方程在D上有解,符合题意.
,此方程在D上有解,符合题意.设过点(-1,
 )的切线切曲线y=f(x)于(x0,x0+
)的切线切曲线y=f(x)于(x0,x0+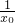 ),则切线的斜率为1-
),则切线的斜率为1-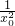 ,
,其方程为y-x0-
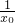 =(1-
=(1-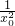 )(x-x0),把点(-1,
)(x-x0),把点(-1, )的坐标代入整理得,
)的坐标代入整理得,5
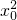 -8x0-4=0,解得x0=-
-8x0-4=0,解得x0=- 或x0=2,
或x0=2,把x0=-
 或x0=2分别代入上述方程得所求的切线方程是:y=-
或x0=2分别代入上述方程得所求的切线方程是:y=-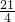 x-5和y=
x-5和y= x+1,
x+1,即21x+4y+20=0和3x-4y+4=0.
(Ⅱ)由(Ⅰ)知f(x)=x+
 ,当n∈N*时,
,当n∈N*时,fn(x)-f(xn)=
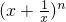 -(xn+
-(xn+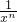 )
)=
 xn-1•
xn-1• +
+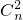 xn-2•
xn-2•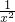 +…+
+…+ x2•
x2• +
+ x•
x•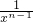
=
 xn-2+
xn-2+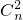 xn-4+…+
xn-4+…+
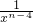 +
+
 ,
,由x∈(0,+∞),n∈N*知,xn∈(0,+∞),那么
2(fn(x)-f(xn))=
 xn-2+
xn-2+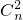 xn-4+…+
xn-4+…+
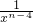 +
+

+

 +
+
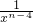 +…+
+…+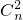 xn-4+
xn-4+ xn-2
xn-2=
 xn-2+
xn-2+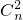 xn-4+…+
xn-4+…+
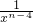 +
+

+

 +
+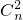
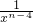 +…+
+…+ xn-4+
xn-4+ xn-2
xn-2=
 (xn-2+
(xn-2+ )+
)+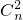 (xn-4+
(xn-4+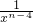 )+…+
)+…+ (xn-2+
(xn-2+ )
)≥2
 +2
+2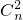 +…+2
+…+2 )
)=2(
 +
+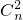 +…+
+…+ )
)=2[(
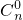 +
+ +
+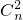 +…+
+…+ +
+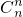 )-
)-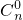 -
-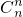 )]
)]=2(2n-2)
所以fn(x)-f(xn)≥2n-2.
分析:(Ⅰ)令x=y=1,可求得f(1)=2,从而可求得f(x)=x+
 ,设过点(-1,
,设过点(-1, )的切线切曲线y=f(x)于(x0,x0+
)的切线切曲线y=f(x)于(x0,x0+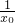 ),则切线的斜率为1-
),则切线的斜率为1-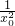 ,于是可求得切线方程,将点(-1,
,于是可求得切线方程,将点(-1, )的坐标代入方程即可求得x0,从而可得过点(-1,
)的坐标代入方程即可求得x0,从而可得过点(-1, )的曲线y=f(x)的切线的一般式方程;
)的曲线y=f(x)的切线的一般式方程;(Ⅱ)由(Ⅰ)知f(x)=x+
 ,当n∈N*时,fn(x)-f(xn)=
,当n∈N*时,fn(x)-f(xn)=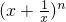 -(xn+
-(xn+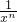 ),利用二项式定理将
),利用二项式定理将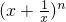 展开,采用倒序相加法可求得2(fn(x)-f(xn)),再利用基本不等式即可证得结论.
展开,采用倒序相加法可求得2(fn(x)-f(xn)),再利用基本不等式即可证得结论.点评:本题考查利用导数研究曲线上某点切线方程,考查不等式的证明,突出二项式定理及倒序相加法与基本不等式的综合运用,属于难题.

练习册系列答案
相关题目
 ;②曲线y=f(x)存在与直线x+y+1=0平行的切线.
;②曲线y=f(x)存在与直线x+y+1=0平行的切线. )的曲线y=f(x)的切线的一般式方程;
)的曲线y=f(x)的切线的一般式方程;