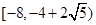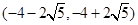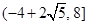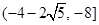题目内容
已知函数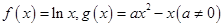 .
.
(1)若函数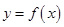 与
与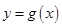 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数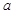 的值及点P的坐标;
的值及点P的坐标;
(2)若函数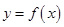 与
与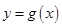 的图象有两个不同的交点M、N,求实数
的图象有两个不同的交点M、N,求实数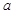 的取值范围 .
的取值范围 .
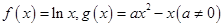 .
.(1)若函数
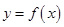 与
与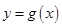 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数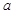 的值及点P的坐标;
的值及点P的坐标;(2)若函数
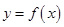 与
与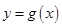 的图象有两个不同的交点M、N,求实数
的图象有两个不同的交点M、N,求实数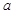 的取值范围 .
的取值范围 .(1)1,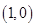 ;(2)
;(2)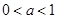 .
.
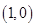 ;(2)
;(2)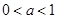 .
.试题分析:(1)先设公共点P坐标,再根据函数解析式在点P出的函数值相等,在点P出的切线斜率相等列方程组,求点P坐标及a的值;(2)根据两函数相等方程求
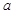 的表达式,再利用导数求表达式的值域,则可得实数
的表达式,再利用导数求表达式的值域,则可得实数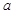 的取值范围.
的取值范围.试题解析:(1)设函数
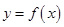 与
与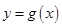 的图象的公共点
的图象的公共点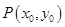 ,
,则有
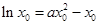 ①又在点P有共同的切线
①又在点P有共同的切线∴
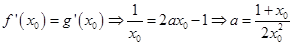 代入①得
代入①得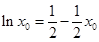 3分
3分设
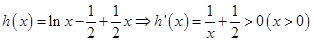
所以函数
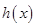 最多只有1个零点,观察得
最多只有1个零点,观察得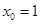 是零点,
是零点,∴
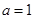 ,此时
,此时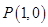 . 3分
. 3分(2)由
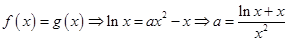 2分
2分令
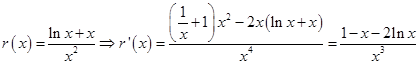 2分
2分当
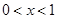 时,
时,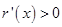 ,则
,则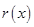 单调递增
单调递增当
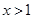 时,
时,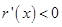 ,则
,则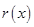 单调递减,且
单调递减,且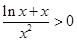
所以
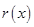 在
在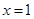 处取到最大值
处取到最大值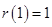 , 2分
, 2分所以要使
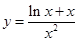 与
与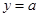 有两个不同的交点,则有
有两个不同的交点,则有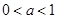 2分
2分
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 R,
R, ,
,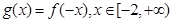 ,若
,若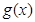 的最小值与
的最小值与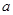 无关,求
无关,求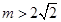 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于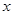 的方程
的方程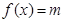 的解集
的解集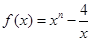 ,且
,且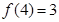 .
.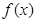 的奇偶性并说明理由;
的奇偶性并说明理由;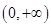 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;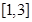 上,不等式
上,不等式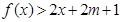 恒成立,试确定实数
恒成立,试确定实数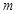 的取值范围.
的取值范围.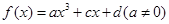 是R上的奇函数,当
是R上的奇函数,当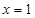 时
时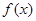 取得极值
取得极值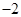 .
.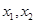
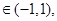 不等式
不等式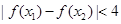 恒成立.
恒成立.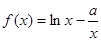 (
(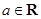 ).
).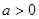 时,判断
时,判断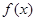 在定义域上的单调性;
在定义域上的单调性;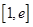 上的最小值为
上的最小值为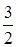 ,求
,求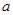 的值;
的值;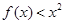 在
在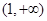 上恒成立,试求
上恒成立,试求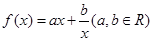 ,若
,若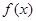 在点
在点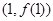 处的切线斜率为
处的切线斜率为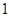 .
.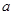 表示
表示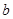 ;
;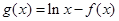 ,若
,若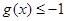 对定义域内的
对定义域内的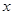 恒成立,求实数
恒成立,求实数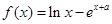 .
.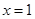 是,
是,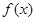 的极值点,讨论
的极值点,讨论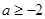 时,证明:
时,证明: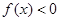 .
.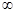 ,
,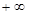 )内有定义,对于给定的正数k,定义函数:
)内有定义,对于给定的正数k,定义函数: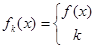
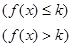 ,取函数
,取函数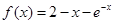 ,若对任意的x∈(-
,若对任意的x∈(-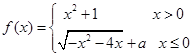 在点(1,2)处的切线与
在点(1,2)处的切线与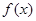 的图像有三个公共点,则
的图像有三个公共点,则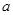 的取值范围是( )
的取值范围是( )