题目内容
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() ,曲线
,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)设 ![]() 为参数,若
为参数,若 ![]() ,求直线
,求直线 ![]() 的参数方程;
的参数方程;
(2)已知直线 ![]() 与曲线
与曲线 ![]() 交于
交于 ![]() ,设
,设 ![]() ,且
,且 ![]() ,求实数
,求实数 ![]() 的值.
的值.
【答案】
(1)解:直线 ![]() 的极坐标方程为
的极坐标方程为 ![]()
所以 ![]() ,即
,即 ![]()
因为 ![]() 为参数,若
为参数,若 ![]() ,代入上式得
,代入上式得 ![]() ,
,
所以直线 ![]() 的参数方程为
的参数方程为 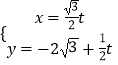 (
( ![]() 为参数)
为参数)
(2)解:由 ![]() ,得
,得 ![]()
由 ![]() 代入,得
代入,得 ![]()
将直线 ![]() 的参数方程与
的参数方程与 ![]() 的直角坐标方程联立
的直角坐标方程联立
得 ![]() (*)
(*)![]()
![]() ,
,
设点 ![]() 分别对应参数
分别对应参数 ![]() 恰为上述方程的根
恰为上述方程的根
则 ![]() ,
,
由题设得 ![]() ,
,
则有 ![]() ,得
,得 ![]() 或
或 ![]()
因为 ![]() ,所以
,所以 ![]() .
.
【解析】(1)直线l的极坐标方程为![]() ,利用互化公式可得直角坐标方程:
,利用互化公式可得直角坐标方程:![]() 设t为参数,即可得出直线l的参数方程,(2)把直线l的参数方程与C的直角坐标方程联立,利用t的几何意义可解得实数a的值.
设t为参数,即可得出直线l的参数方程,(2)把直线l的参数方程与C的直角坐标方程联立,利用t的几何意义可解得实数a的值.
【考点精析】本题主要考查了极坐标系的相关知识点,需要掌握平面内取一个定点O,叫做极点;自极点O引一条射线OX叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系才能正确解答此题.

练习册系列答案
相关题目