题目内容
已知抛物线x2=4y的焦点F和点A(-1,4),P为抛物线上一点,则|PA|+|PF|的最小值是
5
5
.分析:如图所示,由抛物线方程x2=4y,可得
=
=1.进而得到抛物线的焦点F和准线l方程.过点A作AM⊥l,垂足为M,交抛物线与点P.则|PF|=|PM|,此时|PA|+|PF|取得最小值.
| p |
| 2 |
| 4 |
| 4 |
解答:解:如图所示,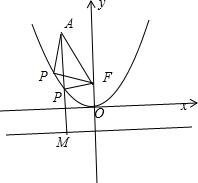
由抛物线方程x2=4y,可得
=
=1.
∴抛物线的焦点F(0,1),准线l方程为y=-1.
过点A作AM⊥l,垂足为M,交抛物线与点P.
则|PF|=|PM|,此时|PA|+|PF|取得最小值=|AM|=4-(-1)=5.
故答案为5.

由抛物线方程x2=4y,可得
| p |
| 2 |
| 4 |
| 4 |
∴抛物线的焦点F(0,1),准线l方程为y=-1.
过点A作AM⊥l,垂足为M,交抛物线与点P.
则|PF|=|PM|,此时|PA|+|PF|取得最小值=|AM|=4-(-1)=5.
故答案为5.
点评:熟练掌握抛物线的定义、三角形的三边大小关系与三点共线是解题的关键.

练习册系列答案
相关题目
 已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.
已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点. (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F. (2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.
(2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.