题目内容
在 中,
中, ,则
,则 ( )
( )
A.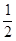 | B. | C. | D. |
A
解析试题分析:由正弦定理可得 即
即 ,在
,在 中,可得
中,可得 ,也就是
,也就是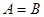 .那么
.那么 ,由余弦定理
,由余弦定理 ,代入可得
,代入可得 ,则
,则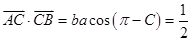 .
.
考点:正余弦定理,向量的数量积运算.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
设 的内角
的内角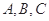 所对边的长分别为
所对边的长分别为 ,若
,若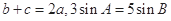 ,则角
,则角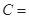 ( )
( )
A.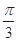 | B.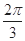 | C.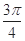 | D.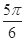 |
在 则
则 ( )
( )
A. | B. | C. | D. |
在△ABC中,角A,B,C所对的边分别是a,b,c,若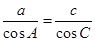 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
若 的三个内角满足
的三个内角满足 ,则
,则 ( )
( )
| A.一定是锐角三角形 | B.一定是直角三角形 |
| C.一定是钝角三角形 | D.可能是锐角三角形,也可能是钝角三角形 |
在 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且 ,则下列关系一定不成立的是( )
,则下列关系一定不成立的是( )
A. | B. | C. | D. |
某人要制作一个三角形,要求它的三条高的长度分别为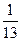 ,
, ,
, ,则此人能( )
,则此人能( )
| A.不能作出这样的三角形 |
| B.作出一个锐角三角形 |
| C.作出一个直角三角形 |
| D.作出一个钝角三角形 |
设△ABC的内角A,B,C所对的边分别为a,b,c.若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则sinA∶sinB∶sinC为( )
| A.4∶3∶2 |
| B.5∶6∶7 |
| C.5∶4∶3 |
| D.6∶5∶4 |
在△ABC中,若∠A=60°,∠B=45°,BC=3 ,则AC等于( )
,则AC等于( )
A.4 | B.2 | C. | D. |