题目内容
7.若a∈[0,1),当x,y满足$\left\{\begin{array}{l}{x-ay-2≤0}\\{x-y+1≥0}\\{2x+y-4≥0}\end{array}\right.$时,z=x+y的最小值为( )| A. | 4 | B. | 3 | C. | 2 | D. | 无法确定 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求目标函数z=x+y的最小值.
解答 解:由x-ay-2=0得ay=x-2,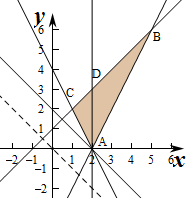
若a=0,则x-2=0,
若0<a<1,则直线方程等价为y=$\frac{1}{a}$x-$\frac{2}{a}$,此时直线斜率k=$\frac{1}{a}$>1,
作出不等式组对应的平面区域如图:(阴影部分).
由z=x+y得y=-x+z,平移直线y=-x+z,
由图象可知当直线y=-x+z经过点A时,
直线y=-x+z的截距最小,此时z最小.
由$\left\{\begin{array}{l}{x-ay-2=0}\\{2x+y-4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$,即A(2,0),代入目标函数z=x+y得z=2.
即目标函数z=x+y的最小值为2.
故选:C.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.已知O、A、B三地在同一水平面内,A地在O地正东方向2km处,B地在O地正北方向2km处,某测绘队员在A、B之间的直线公路上任选一点C作为测绘点,用测绘仪进行测绘,O地为一磁场,距离其不超过$\sqrt{3}$km的范围内会测绘仪等电子仪器形成干扰,使测量结果不准确,则该测绘队员能够得到准确数据的概率是( )
| A. | 1-$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
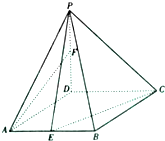 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,0<k<1,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,0<k<1,点F为PD中点.