题目内容
（I）求两条平行直线3x+4y-12=0与mx+8y+6=0之间的距离；（Ⅱ）求两条垂直直线2x+y+2=0与nx+4y-2=0的交点坐标．
分析：（I）先利用平行条件求出m，再由平行线的距离公式，可得结论；
（Ⅱ）由2x+y+2=0与nx+4y-2=0垂直，得n的值，再联立方程组成方程组，求出交点坐标．
（Ⅱ）由2x+y+2=0与nx+4y-2=0垂直，得n的值，再联立方程组成方程组，求出交点坐标．
解答：解：（I）由平行知斜率相等，得m=6，∴mx+8y+6=0为3x+4y+3=0； …（3分）
再由平行线的距离公式，可得d=
=3…（7分）
（Ⅱ）由2x+y+2=0与nx+4y-2=0垂直，得2n+4y=0，∴n=-2，∴nx+4y-2=0为x-2y+1=0；…（10分）
由
得
，
∴交点为（-1，0）…（14分）
再由平行线的距离公式，可得d=
| |3+12| | ||
|
（Ⅱ）由2x+y+2=0与nx+4y-2=0垂直，得2n+4y=0，∴n=-2，∴nx+4y-2=0为x-2y+1=0；…（10分）
由
|
|
∴交点为（-1，0）…（14分）
点评：本题考查两条直线的平行、垂直，考查距离公式，考查学生的计算能力，属于基础题．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
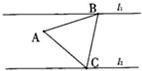在同一平面内，边长为2的等边△ABC的两个顶点B、C分别再两条平行直线l1，l2上，另一个顶点A在直线l1、l2之间，AB与l1的夹角为θ，0o＜θ＜60o．
，焦点F2到渐近线的距离为
，两条准线之间的距离为1。 （I）求此双曲线的方程； （II）过双曲线焦点F1的直线与双曲线的两支分别相交于A、B两点，过焦点F2且与AB平行的直线与双曲线分别相交于C、D两点，若A、B、C、D这四点依次构成平行四边形ABCD，且
，求直线AB的方程。