题目内容
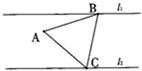 在同一平面内,边长为2的等边△ABC的两个顶点B、C分别再两条平行直线l1,l2上,另一个顶点A在直线l1、l2之间,AB与l1的夹角为θ,0o<θ<60o.
在同一平面内,边长为2的等边△ABC的两个顶点B、C分别再两条平行直线l1,l2上,另一个顶点A在直线l1、l2之间,AB与l1的夹角为θ,0o<θ<60o.(I)当θ=45o时,求点A到直线l1的距离;
(II)若点A到直线l1、l2的距离分别为d1、d2,记d1•d2=f(θ),求f(θ)的取值范围.
分析:(I)过点A作直线l1的垂线,垂足为M,然后解三角形,求点A到直线l1的距离;
(II)过点A作直线l2的垂线,垂足为N,点A到直线l1、l2的距离分别为d1、d2,表示出d1、d2,和d1•d2=f(θ),然后求f(θ)的取值范围.
(II)过点A作直线l2的垂线,垂足为N,点A到直线l1、l2的距离分别为d1、d2,表示出d1、d2,和d1•d2=f(θ),然后求f(θ)的取值范围.
解答:解:(I)过点A作直线l1的垂线,垂足为M,
在Rt△ABM中,sin45°=
,
∴|AM|=2sin45°=2×
=
即:点A到直线l1的距离为
.
(II)过点A作直线l2的垂线,垂足为N,
∵AB与l2的夹角为θ,∴AC与l2的夹角为60°-θ,
在Rt△ABM,d1=AM=2sinθ
在Rt△ACN,d2=AN=2sin(60°-θ)
d1•d2═4sin(60°-θ)sinθ
=4(
cosθ-
sinθ)sinθ
=2(
sin2θ-
sin2θ)
=2sin(2θ+30°)-1
∵0°<θ<60°∴30°<2θ+30°<150°
∴
<sin(2θ+30°)≤1,∴d1d2∈(0,1]
在Rt△ABM中,sin45°=
| |AM| |
| 2 |
∴|AM|=2sin45°=2×
| ||
| 2 |
| 2 |
即:点A到直线l1的距离为
| 2 |
(II)过点A作直线l2的垂线,垂足为N,
∵AB与l2的夹角为θ,∴AC与l2的夹角为60°-θ,
在Rt△ABM,d1=AM=2sinθ
在Rt△ACN,d2=AN=2sin(60°-θ)
d1•d2═4sin(60°-θ)sinθ
=4(
| ||
| 2 |
| 1 |
| 2 |
=2(
| ||
| 2 |
| 1-cos2θ |
| 2 |
=2sin(2θ+30°)-1
∵0°<θ<60°∴30°<2θ+30°<150°
∴
| 1 |
| 2 |
点评:本题考查点到直线的距离,正弦函数的定义域和值域,考查学生的计算能力,是中档题.

练习册系列答案
相关题目
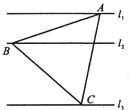 如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,边长为4的正三角形的三顶点分别在l1、l2、l3上,则l2与l3间的距离是( )
如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,边长为4的正三角形的三顶点分别在l1、l2、l3上,则l2与l3间的距离是( )A、2
| ||||
B、
| ||||
C、
| ||||
D、2
|
