题目内容
设函数f(x)=xsinx在x=x0处取得极值,则(1+x02)cos2x0的值为( )
| A.0 | B.1 | C.2 | D.3 |
f(x)=xsinx则f′(x)=sinx+xcosx=0
解得tanx=-x,
∴x02=tan2x0,
∴(x02+1)cos2x0=(tan2x0+1)cos2x0=
×cos2x0=1
故答案为:1.
解得tanx=-x,
∴x02=tan2x0,
∴(x02+1)cos2x0=(tan2x0+1)cos2x0=
| cos2x0+sin2x0 |
| cos2x0 |
故答案为:1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

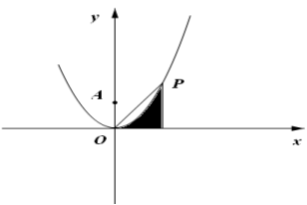
 ,点
,点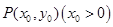 在曲线
在曲线 上,若阴影部分面积与
上,若阴影部分面积与 面积相等,则
面积相等,则 =________
=________
 ,则
,则 的大小关系为( )
的大小关系为( )


