题目内容
若z∈C,arg(z2-4)=
,arg(z2+4)=
,则z的值是
| 5π |
| 6 |
| π |
| 3 |
±(1+
i)
| 3 |
±(1+
i)
.| 3 |
分析:设z=x+yi(x、y∈R),算出z2-4=(x2-y2-4)+2xyi,z2+4=(x2-y2+4)+2xyi.根据复数辐角主值的定义,得关于x、y的方程组,解得x、y的值,即得z=1+
i或z=-1-
i.
| 3 |
| 3 |
解答:解:设z=x+yi(x、y∈R),则z2=(x+yi)2=(x2-y2)+2xyi
∴z2-4=(x2-y2-4)+2xyi,z2+4=(x2-y2+4)+2xyi,
∵arg(z2-4)=
,arg(z2+4)=
,
∴tan
=
=-
…①,tan
=
=
…②.
联解①②,得
或
,所以z=1+
i或z=-1-
i
故答案为:±(1+
i)
∴z2-4=(x2-y2-4)+2xyi,z2+4=(x2-y2+4)+2xyi,
∵arg(z2-4)=
| 5π |
| 6 |
| π |
| 3 |
∴tan
| 5π |
| 6 |
| 2xy |
| x2-y2-4 |
| ||
| 3 |
| π |
| 3 |
| 2xy |
| x2-y2+4 |
| 3 |
联解①②,得
|
|
| 3 |
| 3 |
故答案为:±(1+
| 3 |
点评:本题给出复数z2-4、z2+4的辐角主值,求复数z的值,着重考查了复数的四则运算和辐角的定义等知识,属于基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 是实数,则正整数n的最小值是4
是实数,则正整数n的最小值是4 ∈
∈
 都是非零复数,
都是非零复数,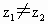 ,且复平面上O为原点,点A和B分别与
,且复平面上O为原点,点A和B分别与 和
和 对应,∠AOB=
对应,∠AOB= ,则
,则
 |≤1,则
|≤1,则 ≤arg(-zi)≤
≤arg(-zi)≤ ,其中真命题是
,其中真命题是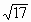 ,|z-2|=4,则z=________;设z∈C,arg(z+3)=
,|z-2|=4,则z=________;设z∈C,arg(z+3)=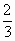 π,arg(z-5)=
π,arg(z-5)=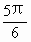 ,则z=________.
,则z=________.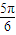 ,arg(z2+4)=
,arg(z2+4)=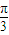 ,则z的值是 .
,则z的值是 .