题目内容
设复数z=x+(4-x)i(x∈R).
(Ⅰ)若复数
为纯虚数,求x的值;
(Ⅱ)若存在x∈[-1,3],使得|z|2-2m≥0,求实数m的取值范围.
(Ⅰ)若复数
| z | 1-i |
(Ⅱ)若存在x∈[-1,3],使得|z|2-2m≥0,求实数m的取值范围.
分析:(Ⅰ)把z=x+(4-x)i代入
,整理为a+bi(a,b∈R)的形式由实部等于0,虚部不等于0求解x得值;
(Ⅱ)把|z|2-2m≥0变形为2m≤|z|2,代入复数z后变为m≤(x-2)2+4,求出不等式右边代数式在x∈[-1,3]的最大值,由m小于等于该最大值即可得到实数m的取值范围.
| z |
| 1-i |
(Ⅱ)把|z|2-2m≥0变形为2m≤|z|2,代入复数z后变为m≤(x-2)2+4,求出不等式右边代数式在x∈[-1,3]的最大值,由m小于等于该最大值即可得到实数m的取值范围.
解答:解:(Ⅰ)因为
=
=
=(x-2)+2i
又因为复数
为纯虚数,所以x-2=0,即x=2;
(Ⅱ)由|z|2-2m≥0得,2m≤|z|2=x2+(4-x)2=2x2-8x+16=2(x-2)2+8,
即m≤(x-2)2+4,
因为x∈[-1,3],所以当x=-1时(x-2)2+4的最大值为13,
又因为存在x∈[-1,3],使得|z|2-2m≥0,
所以实数m的取值范围是m≤13.
| z |
| 1-i |
| x+(4-x)i |
| 1-i |
| [x+(4-x)i](1+i) |
| 2 |
又因为复数
| z |
| 1-i |
(Ⅱ)由|z|2-2m≥0得,2m≤|z|2=x2+(4-x)2=2x2-8x+16=2(x-2)2+8,
即m≤(x-2)2+4,
因为x∈[-1,3],所以当x=-1时(x-2)2+4的最大值为13,
又因为存在x∈[-1,3],使得|z|2-2m≥0,
所以实数m的取值范围是m≤13.
点评:本题考查了复数代数形式的乘除运算,考查了复数的模,训练了分离变量法和配方法求二次函数的最值,解答此题的关键是把求使得|z|2-2m≥0成立的实数m的取值范围转化为m小于等于二次三项式的最大值,该题是中档题.

练习册系列答案
相关题目
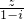 为纯虚数,求x的值;
为纯虚数,求x的值;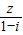 为纯虚数,求x的值;
为纯虚数,求x的值;