题目内容
对角线互相垂直的空间四边形ABCD各边中点分别为M、N、P、Q,则四边形MNPQ是分析:利用三角形的中位线定理可得:四边形MNPQ为平行四边形,再利用异面直线所成的角证明MN⊥MQ即可得出.
解答:解:如图所示.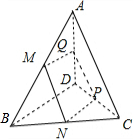
∵点M、N、P、Q分别是四条边的中点,
∴MN
AC,PQ
AC,
∴四边形MNPQ是平行四边形.
又∵BD∥MQ,AC⊥BD,
∴MN⊥MQ,
∴平行四边形MNPQ是矩形.
故答案为:矩形.

∵点M、N、P、Q分别是四条边的中点,
∴MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴四边形MNPQ是平行四边形.
又∵BD∥MQ,AC⊥BD,
∴MN⊥MQ,
∴平行四边形MNPQ是矩形.
故答案为:矩形.
点评:本题考查了三角形的中位线定理、平行四边形的判定定理、异面直线所成的角、矩形的判定,属于基础题.

练习册系列答案
相关题目