题目内容
在平面几何中,关于四边形有下面的结论:
①顺次连结对角线相等的四边形四边中点得到的四边形是菱形;
②顺次连结对角线互相垂直的四边形四边中点得到的四边形是矩形;
③顺次连结对角线相等且互相垂直的四边形四边中点得到的四边形是正方形.
请思考并回答下面两个问题:
(1)如果一个四边形是空间四边形,上述结论还成立吗?也就是上述平面几何中的结论能推广到空间几何中吗?
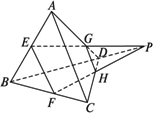
(2)空间四边形ABCD中,E、F分别为AB、BC的中点,DG∶GA=DH∶HC=1∶3,EF和GH有何位置关系?设直线EG与FH交于点P,那么点B、D、P共线吗?
答案:
解析:
提示:
解析:
|
通过三角形中位线的性质应用,可以将上述三个结论推广到空间四边形,即这三个结论在空间四边形中依然成立.如图,用运动的观点来观察这个图形.如果E、F、G、H都是中点,可以证明BD与平面EFGH没有交点(即平行).如果GH保持与AC平行且向点D逐渐靠近时,直线EG、FH与BD就不再平行,而是交于点P,同时点P一定在直线BD上,也逐渐向点D靠近.
|
提示:
|
在平面四边形中,是以三角形中位线为桥梁来证明上述三个结论的.在空间四边形中,同样可以以空间四边形的对角线AC与BD的关系为桥梁来证明上述三个结论. |

练习册系列答案
相关题目
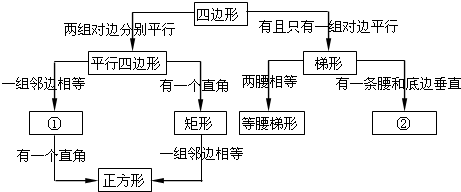
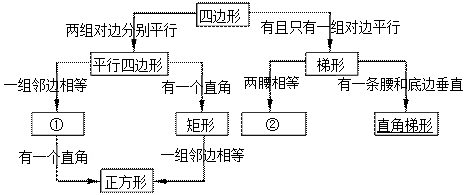
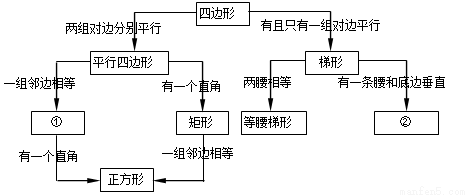
 关系可用以下框图描述:
关系可用以下框图描述: