题目内容
(8分)有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)共有多少种放法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有两个盒不放球,有多少种放法?
【答案】
(1)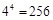 ;(2)
;(2)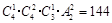 ;(3)
;(3) .
.
【解析】(1)利用分布乘法原理求解即可;(2)先选一个特称的盒子,然后利用分步原理求解;(3)先二个特殊盒子,然后把球分堆,最后利用分布乘法原理求解即可。
解:(1)一个球一个球地放到盒子里去,每只球都可有4种独立的放法,由分步乘法计数原理,放法共有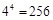 种.
种.
(2)为保证“恰有一个盒子不放球”,先从四个盒子中任意拿出去1个,即将4个球分成2,1,1的三组,有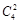 种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法:
种分法;然后再从三个盒子中选一个放两个球,其余两个球,两个盒子,全排列即可.由分步乘法计数原理,共有放法: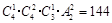 种.
种.
(3)先从四个盒子中任意拿走两个有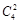 种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有
种,问题转化为:“4个球,两个盒子,每盒必放球,有几种放法?”从放球数目看,可分为(3,1),(2,2)两类.第一类:可从4个球中先选3个,然后放入指定的一个盒子中即可,有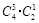 种放法;第二类:有
种放法;第二类:有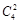 种放法.因此共有
种放法.因此共有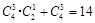 种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有:
种.由分步乘法计数原理得“恰有两个盒子不放球”的放法有: 种.
种.

练习册系列答案
相关题目
 (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
. 、
、 的值;
的值;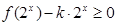 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;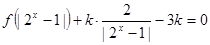 有三个不同的实数解,求实数
有三个不同的实数解,求实数 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。 与
与 的关系为
的关系为 ;
; ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。 为
为 上偶函数,当
上偶函数,当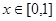 时
时 ,又函数
,又函数 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。