题目内容
6．求值：$\frac{cos40°+sin50°（1+\sqrt{3}tan10°）}{sin70°\sqrt{1+cos40°}}$．分析 化切为弦，然后利用两角和与差的正弦及二倍角余弦公式化简求值．
解答 解：$\frac{cos40°+sin50°（1+\sqrt{3}tan10°）}{sin70°\sqrt{1+cos40°}}$
=$\frac{cos40°+sin50°\frac{\sqrt{3}sin10°+cos10°}{cos10°}}{\sqrt{2}sin70°cos20°}$
=$\frac{cos40°+\frac{sin50°}{cos10°}•2（sin10°cos30°+cos10°sin30°）}{\sqrt{2}sin70°cos20°}$
=$\frac{cos40°+\frac{2sin50°sin40°}{cos10°}}{\sqrt{2}sin70°cos20°}$
=$\frac{cos40°+\frac{sin80°}{cos10°}}{\sqrt{2}sin70°cos20°}$
=$\frac{cos40°+1}{\sqrt{2}co{s}^{2}20°}$
=$\frac{2co{s}^{2}20°}{\sqrt{2}co{s}^{2}20°}$
=$\sqrt{2}$．
点评 本题考查三角函数的化简求值，考查了两角和与差的正弦及二倍角余弦公式，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．在△ABC中，已知a-b=ccosB-ccosA，则△ABC的形状是（ ）
| A． | 等腰三角形 | B． | 直角三角形 | ||
| C． | 等边三角形 | D． | 等腰或直角三角形 |
17．执行如图所示的程序框图输出的结果为（ ）
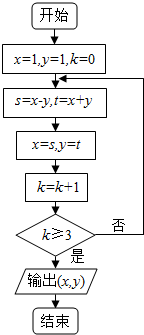
| A． | （-2，2） | B． | （-4，0） | C． | （-4，-4） | D． | （0，-8） |
11．下列命题中，正确的是（ ）
| A． | {0}是空集 | B． | {x∈Q|$\frac{6}{x}$∈N}是有限集 | ||
| C． | {x∈Q|x2+x+2=0}是空集 | D． | {1，2}和{2，1}是不同的集合 |