题目内容
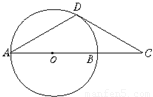
 如图,已知C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
如图,已知C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
证明:连接OD,
∵AD=CD,∴∠A=∠C=30°
又∵OD=OA,∴∠A=∠ODA=30°
∴∠DOC=60°,∴∠ODC=90°
又OD⊥CD,
∴DC是⊙O的切线.
分析:做出辅助线,连接OD,根据AD=CD,得到∠A=∠C=30°,根据角的等量代换,得到∠ODC=90°,即OD⊥CD,得到结论.
点评:本题考查证明圆的切线的问题,本题解题的关键是做出辅助线,证出圆心与切点的连线垂直与切线,本题是一个基础题.
∵AD=CD,∴∠A=∠C=30°
又∵OD=OA,∴∠A=∠ODA=30°
∴∠DOC=60°,∴∠ODC=90°
又OD⊥CD,
∴DC是⊙O的切线.
分析:做出辅助线,连接OD,根据AD=CD,得到∠A=∠C=30°,根据角的等量代换,得到∠ODC=90°,即OD⊥CD,得到结论.
点评:本题考查证明圆的切线的问题,本题解题的关键是做出辅助线,证出圆心与切点的连线垂直与切线,本题是一个基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
 22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点. 如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10.
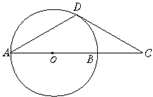
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10. 如图,已知C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.
如图,已知C是⊙O的直径AB的延长线上的一点,D是⊙O上的一点且AD=CD,∠C=30°,求证:DC是⊙O的切线.